Friedel Oscillations疑问
问题
动量空间中电势为
$$\begin{align} \varphi (\vec{q})= \frac{\varphi_{ext(\vec{q})}}{\varepsilon(\vec{q})} \end{align}$$其中
$$\begin{align} \varphi_{ext}(\vec{q}) = \frac{-e}{\varepsilon_0 V q^2 } \end{align}$$所以
\begin{equation} \label{eq:1} \varphi (\vec{q})= \frac{-e}{\varepsilon_0 V q^2 {\varepsilon(\vec{q})}} \end{equation}
Thomas-Fermi 近似的结果
Thomas-Fermi 近似给出
$$\begin{align} \varepsilon_{TF}(\vec{q}) = 1 +\frac{q_{TF}^2}{q^2} \end{align}$$将上式代入 $\varphi(\vec{q})$ 有
\begin{equation} \varphi (\vec{q})= \frac{-e}{\varepsilon_0 V q^2 \left(1 +\frac{q_{TF}^2}{q^2}\right)} =\frac{-e}{\varepsilon_0 V \left(q^2 +q_{TF}^2\right)} \end{equation}
对其 Fourier Transform
$$\begin{align} \varphi(\vec{r}) =& \int_{-\infty}^{+\infty} e^{i \vec{q}\cdot \vec{r}} \varphi (\vec{q}) \mathrm{d}^3 q \\ =& \frac{-e}{2 \pi^2 \varepsilon_0} \cdot \frac{1}{r} \int_0^{+\infty} \sin(qr)\cdot \frac{q}{q^2+q_{TF}^2} \mathrm{d}q\\ =& \frac{-e}{4 \pi \varepsilon_0} \cdot \frac{1}{r} \cdot \frac{2}{\pi}\int_0^{+\infty} \sin(qr)\cdot \frac{q}{q^2+q_{TF}^2} \mathrm{d}q \end{align}$$对
$$\begin{align} \frac{q}{q^2+q_{TF}^2} \end{align}$$在 $q \rightarrow +\infty$ 展开(与在 $q_{TF}\rightarrow 0$ 时对 $q_{TF}$ 展开相同):
import sympy as sym
q = sym.Symbol('q')
q_tf = sym.Symbol('q_TF')
s = sym.series(q/(q**2+q_tf**2),q,sym.oo,5)
print(sym.latex(s))- \frac{q_{TF}^{2}}{q^{3}} + \frac{1}{q} + O\left(\frac{1}{q^{5}}; q\rightarrow \infty\right)
$$\begin{align} \frac{q}{q^2+q_{TF}^2} =\frac{q_{TF}^{2}}{q^{3}} + \frac{1}{q} + O\left(\frac{1}{q^{5}}; q\rightarrow \infty\right) \end{align}$$计算 leading order
$$\begin{align} \int_0^{+\infty} \sin(qr)\cdot \frac{1}{q}\mathrm{d}q = \frac{1}{2i} \int_{-\infty}^{+\infty} e^{iqr}\cdot \frac{1}{q} \mathrm{d} q = \frac{1}{2i} \cdot \pi i \cdot 1 = \frac{\pi}{2} \end{align}$$这正好是精确结果
$$\begin{align} \frac{-e}{4 \pi \varepsilon_0} \cdot \frac{e^{-q_{TF} r}}{r} \end{align}$$在 $q_{TF}\rightarrow 0$ 时对 $q_{TF}$ 展开的结果的 leading order 相同.
问题1
Thomas-Fermi 近似结果与精确结果的 $q_{TF}^2$ 的系数不同?
答: 因为展开后的结果中出现了发散项, 所以问题本身就不能展开.
问题2
为什么要对 $q$ 在 $q\rightarrow +\infty$ 展开? 积分的区间不是整个实轴吗?
答: 我之前对展开的目的理解有误. 展开的目的不是为了一阶一阶地计算积分. 展开目的是为了数值的计算积分. Thomas-Fermi 的积分本身可以精确解出, 没必要数值积分, 因此不必做展开. 展开的意义会在下面 RPA 的计算过程中体现.
RPA 的结果
RPA 给出
$$\begin{align} \varepsilon (\vec{q}) = 1+ \frac{q_{TF}^2}{q^2}g\left( \frac{q}{2k_F} \right) \end{align}$$将上式代入 $\phi (\vec{q})$ 有
\begin{equation} \varphi (\vec{q})= \frac{-e}{\varepsilon_0 V q^2 \left(1 +\frac{q_{TF}^2}{q^2}\right)} =\frac{-e}{\varepsilon_0 V \left(q^2 +q_{TF}^2 g\left( \frac{q}{2k_F} \right) \right)} \end{equation}
其中
$$\begin{align} g(u) = \frac{1}{2} \left( 1+\frac{1}{2u}(1-u^2)\ln \left| \frac{1+u}{1-u} \right| \right) \end{align}$$对 $\phi (\vec{q})$ 作 Fourier Transform
$$\begin{align} \varphi(\vec{r}) =\frac{-e}{2 \pi^2 \varepsilon_0} \cdot \frac{1}{r} \int_0^{+\infty} \sin(qr)\cdot \frac{q}{q^2+q_{TF}^2g( \frac{q}{2k_F} )} \mathrm{d}q \end{align}$$级数展开
对
$$\begin{align} \frac{q}{q^2+q_{TF}^2g( \frac{q}{2k_F} )} \end{align} $$在 $q\rightarrow +\infty$ 展开
import sympy as sym
q = sym.Symbol('q')
q_tf = sym.Symbol('q_TF')
kf = sym.Symbol('k_F')
u = q/(2*kf)
*g=1
g = sym.Rational(1,2)*( 1+(1-u**2)/(2*u)*sym.log((u+1)/(u-1) ) )
s = sym.series(q/(q**2+q_tf**2)*g,q,sym.oo,10)
print(sym.latex(s))- \frac{\frac{256 k_{F}^{8}}{63} - \frac{64 k_{F}^{6} q_{TF}^{2}}{35} + \frac{16 k_{F}^{4} q_{TF}^{4}}{15}}{q^{9}} + \frac{\frac{64 k_{F}^{6}}{35} - \frac{16 k_{F}^{4} q_{TF}^{2}}{15} + \frac{4 k_{F}^{2} q_{TF}^{4}}{3}}{q^{7}} + \frac{\frac{16 k_{F}^{4}}{15} - \frac{4 k_{F}^{2} q_{TF}^{2}}{3}}{q^{5}} + \frac{4 k_{F}^{2}}{3 q^{3}} + O\left(\frac{1}{q^{10}}; q\rightarrow \infty\right)
$$\begin{align} \frac{q}{q^2+q_{TF}^2g( \frac{q}{2k_F} )} = \frac{\frac{256 k_{F}^{8}}{63} - \frac{64 k_{F}^{6} q_{TF}^{2}}{35} + \frac{16 k_{F}^{4} q_{TF}^{4}}{15}}{q^{9}} + \frac{\frac{64 k_{F}^{6}}{35} - \frac{16 k_{F}^{4} q_{TF}^{2}}{15} + \frac{4 k_{F}^{2} q_{TF}^{4}}{3}}{q^{7}} + \frac{\frac{16 k_{F}^{4}}{15} - \frac{4 k_{F}^{2} q_{TF}^{2}}{3}}{q^{5}} + \frac{4 k_{F}^{2}}{3 q^{3}} + O\left(\frac{1}{q^{10}}; q\rightarrow \infty\right) \end{align}$$问题3: 接下来该怎么做? 所有的展开项代入积分都是发散的.
答: 展开算错了. 程序中把公式抄错了. 看来最好还是手算 check 一下比较好, 不然不会出现这么低级的错误. 级数展开的计算能力还有待提高...
正确的级数展开
import sympy as sym
q = sym.Symbol('q')
q_tf = sym.Symbol('q_TF')
kf = sym.Symbol('k_F')
u = q/(2*kf)
g = sym.Rational(1,2)*( 1+(1-u**2)/(2*u)*sym.log(sym.Abs((u+1)/(u-1)) ) )
s = sym.series(q/(q**2+q_tf**2*g),q,sym.oo,10)
print(sym.latex(s))- \frac{1}{q} - \frac{4 k_{F}^{2} q_{TF}^{2}}{3 q^{5}} - \frac{16 k_{F}^{4} q_{TF}^{2}}{15 q^{7}} - \frac{64 k_{F}^{6} q_{TF}^{2}}{35 q^{9}} + O\left(\frac{1}{q^{10}}; q\rightarrow \infty\right)
$$\begin{align} \frac{q}{q^2+q_{TF}^2g( \frac{q}{2k_F} )} = \frac{1}{q} - \frac{4 k_{F}^{2} q_{TF}^{2}}{3 q^{5}} - \frac{16 k_{F}^{4} q_{TF}^{2}}{15 q^{7}} - \frac{64 k_{F}^{6} q_{TF}^{2}}{35 q^{9}} + O\left(\frac{1}{q^{10}}; q\rightarrow \infty\right) \end{align}$$数值计算 RPA 的结果
问题分析
首先, 积分
$$\begin{align} \varphi(\vec{r}) =\frac{-e}{2 \pi^2 \varepsilon_0} \cdot \frac{1}{r} \int_0^{+\infty} \sin(qr)\cdot \frac{q}{q^2+q_{TF}^2g( \frac{q}{2k_F} )} \mathrm{d}q \end{align}$$难以解析地计算, 因此想要数值地计算.
其次, 被积函数收敛不够快.
经过前面对被积函数级数展开的分析, 发现被积分函数在远处的 leading order 为
\begin{equation} \label{eq:leading} \frac{\sin(qr)}{q} \end{equation}
也就是说, 被积函数在远处的贡献主要来自于 leading order 项 (\ref{eq:leading}), 而且这一项是可以解析地计算出结果的. 如果我们从被函数中把这项减去, 那么被积函数在远处就近似为 $0$ 了, 也就是说积分会更快地收敛. 这就解决了积分收敛不够快的问题.
构造新的被积函数
构造函数
\begin{equation} F(q) = \sin(qr)\cdot \frac{q}{q^2+q_{TF}^2g( \frac{q}{2k_F} )} - \frac{\sin(qr)}{q} \end{equation}
新的 $F(q)$ 函数会很快地收敛.
原来的积分就可以分解为
$$\begin{align} \varphi(\vec{r}) =&\frac{-e}{2 \pi^2 \varepsilon_0} \cdot \frac{1}{r} \int_0^{+\infty} \sin(qr)\cdot \frac{q}{q^2+q_{TF}^2g( \frac{q}{2k_F} )} \mathrm{d}q \\ =& \frac{-e}{2 \pi^2 \varepsilon_0} \cdot \frac{1}{r} \int_0^{+\infty} \left( F(q) + \frac{\sin(qr)}{q} \right)\mathrm{d}q \\ =& \frac{-e}{2 \pi^2 \varepsilon_0} \cdot \frac{1}{r} \left( \int_0^{+\infty} F(q) \mathrm{d}q + \frac{\pi}{2} \right) \end{align}$$数值积分
下面数值地计算
$$\begin{align} \int_0^{+\infty} F(q) \mathrm{d}q \end{align}$$python 程序如下
#导入数值计算包, 画图包, 积分包
import numpy as np
import matplotlib.pyplot as plt
from scipy import integrate
#设置物理参量
qtf = 3/4
kf = 1/2
#数值积分的区间:(0,end)
end = 5
#定义函数 phi_r, g(u), phi_q, lo(q)是phi_q 的 leading order, F(q)是从 phi(q) 里边减去 leading order
def phi_r(r):
def g(u):
return 1/2*(1+1/(2*u)*(1-u**2)*np.log(np.abs((1+u)/(1-u))))
def phi(q):
phi = np.sin(q*r)*q/(q**2+qtf**2*g(q/(2*kf)))
return phi
def lo(q):
lo = np.sin(q*r)/q
return lo
def F(q):
F = phi(q) - lo(q)
return F
(Fres,err) = integrate.quad(F,0,end)
phir = Fres + np.pi/2
return phir
#计算N个不同的 r 的取值的数值积分
N = 100
#画六个图中的第一个图
plt.subplot(321) #(321)的意思是整个图是3行2列,这个图画在第1个位置
a = 0.1 #画图的区间为[a,b],这里第一个图为 r 取 [0,10]
b = a+10
r = np.linspace(a,b,N)
#进行 N 次数值积分, 然后把 N 个点的数值积分的结果保存在数组 s 中
s = np.linspace(0,0,N)
for i in range(N):
s[i-1] = phi_r(r[i-1])
#画图, 指定线的颜色和图例
plt.plot(r, s, color="red", label="Numerical Result")
#我们想要将数值的结果和 Friedel Oscillations 的结果做比较, 但它们之间会差一个常数k, 现在把这个常数 k 取 N 次数值积分中第一个点的比值
k = phi_r(a)/(1/(a**3)*np.cos(2*kf*a))
fo = k*1/(r**3)*np.cos(2*kf*r) #这是 Friedel Oscillations 的结果
plt.plot(r,fo, "--", color="blue", label="Friedel Oscillation") #画出 Friedel Oscillations 的结果
plt.xlabel("$r$") #设置横坐标的物理量
plt.ylabel("$\phi(r)$") #设置纵坐标的物理量
#以下三行是为了让坐标的数值以科学计数法显示
ax = plt.gca() # 获取当前图像的坐标轴信息
ax.yaxis.get_major_formatter().set_powerlimits((0,1)) # 将坐标轴的base number设置为一位。
plt.legend()
#与画第一个图同样的方法, 画出剩下的5个图, 它们的区别在于 r 的区间不同
plt.subplot(322)
a = 10
b = a+10
r = np.linspace(a,b,N)
s = np.linspace(0,0,N)
for i in range(N):
s[i-1] = phi_r(r[i-1])
plt.plot(r, s, color="red", label="Numerical Result")
k = phi_r(a)/(1/(a**3)*np.cos(2*kf*a))
fo = k*1/(r**3)*np.cos(2*kf*r)
plt.plot(r,fo, "--", color="blue", label="Friedel Oscillation")
plt.xlabel("$r$")
plt.ylabel("$\phi(r)$")
ax = plt.gca() # 获取当前图像的坐标轴信息
ax.yaxis.get_major_formatter().set_powerlimits((0,1)) # 将坐标轴的base number设置为一位。
plt.subplot(323)
a = 20
b = a+10
r = np.linspace(a,b,N)
s = np.linspace(0,0,N)
for i in range(N):
s[i-1] = phi_r(r[i-1])
plt.plot(r, s, color="red", label="Numerical Result")
k = phi_r(a)/(1/(a**3)*np.cos(2*kf*a))
fo = k*1/(r**3)*np.cos(2*kf*r)
plt.plot(r,fo, "--", color="blue", label="Friedel Oscillation")
plt.xlabel("$r$")
plt.ylabel("$\phi(r)$")
ax = plt.gca() # 获取当前图像的坐标轴信息
ax.yaxis.get_major_formatter().set_powerlimits((0,1)) # 将坐标轴的base number设置为一位。
plt.subplot(324)
a = 50
b = a+10
r = np.linspace(a,b,N)
s = np.linspace(0,0,N)
for i in range(N):
s[i-1] = phi_r(r[i-1])
plt.plot(r, s, color="red", label="Numerical Result")
k = phi_r(a)/(1/(a**3)*np.cos(2*kf*a))
fo = k*1/(r**3)*np.cos(2*kf*r)
plt.plot(r,fo, "--", color="blue", label="Friedel Oscillation")
plt.xlabel("$r$")
plt.ylabel("$\phi(r)$")
ax = plt.gca() # 获取当前图像的坐标轴信息
ax.yaxis.get_major_formatter().set_powerlimits((0,1)) # 将坐标轴的base number设置为一位。
plt.subplot(325)
a = 100
b = a+10
r = np.linspace(a,b,N)
s = np.linspace(0,0,N)
for i in range(N):
s[i-1] = phi_r(r[i-1])
plt.plot(r, s, color="red", label="Numerical Result")
k = phi_r(a)/(1/(a**3)*np.cos(2*kf*a))
fo = k*1/(r**3)*np.cos(2*kf*r)
plt.plot(r,fo, "--", color="blue", label="Friedel Oscillation")
plt.xlabel("$r$")
plt.ylabel("$\phi(r)$")
ax = plt.gca() # 获取当前图像的坐标轴信息
ax.yaxis.get_major_formatter().set_powerlimits((0,1)) # 将坐标轴的base number设置为一位。
plt.subplot(326)
a = 200
b = a+10
r = np.linspace(a,b,N)
s = np.linspace(0,0,N)
for i in range(N):
s[i-1] = phi_r(r[i-1])
plt.plot(r, s, color="red", label="Numerical Result")
k = phi_r(a)/(1/(a**3)*np.cos(2*kf*a))
fo = k*1/(r**3)*np.cos(2*kf*r)
plt.plot(r,fo, "--", color="blue", label="Friedel Oscillation")
plt.xlabel("$r$")
plt.ylabel("$\phi(r)$")
ax = plt.gca() # 获取当前图像的坐标轴信息
ax.yaxis.get_major_formatter().set_powerlimits((0,1)) # 将坐标轴的base number设置为一位。
plt.suptitle("The Results of RPA") #画出整个图的标题
plt.show() #显示图片#+RESULTS: : None
结果对比
将数值结果与 Friedel Oscillations 的结果
$$\begin{align} \varphi(\vec{r}) \sim \frac{1}{r^3} \cos (2 k_fr) \end{align}$$进行对比
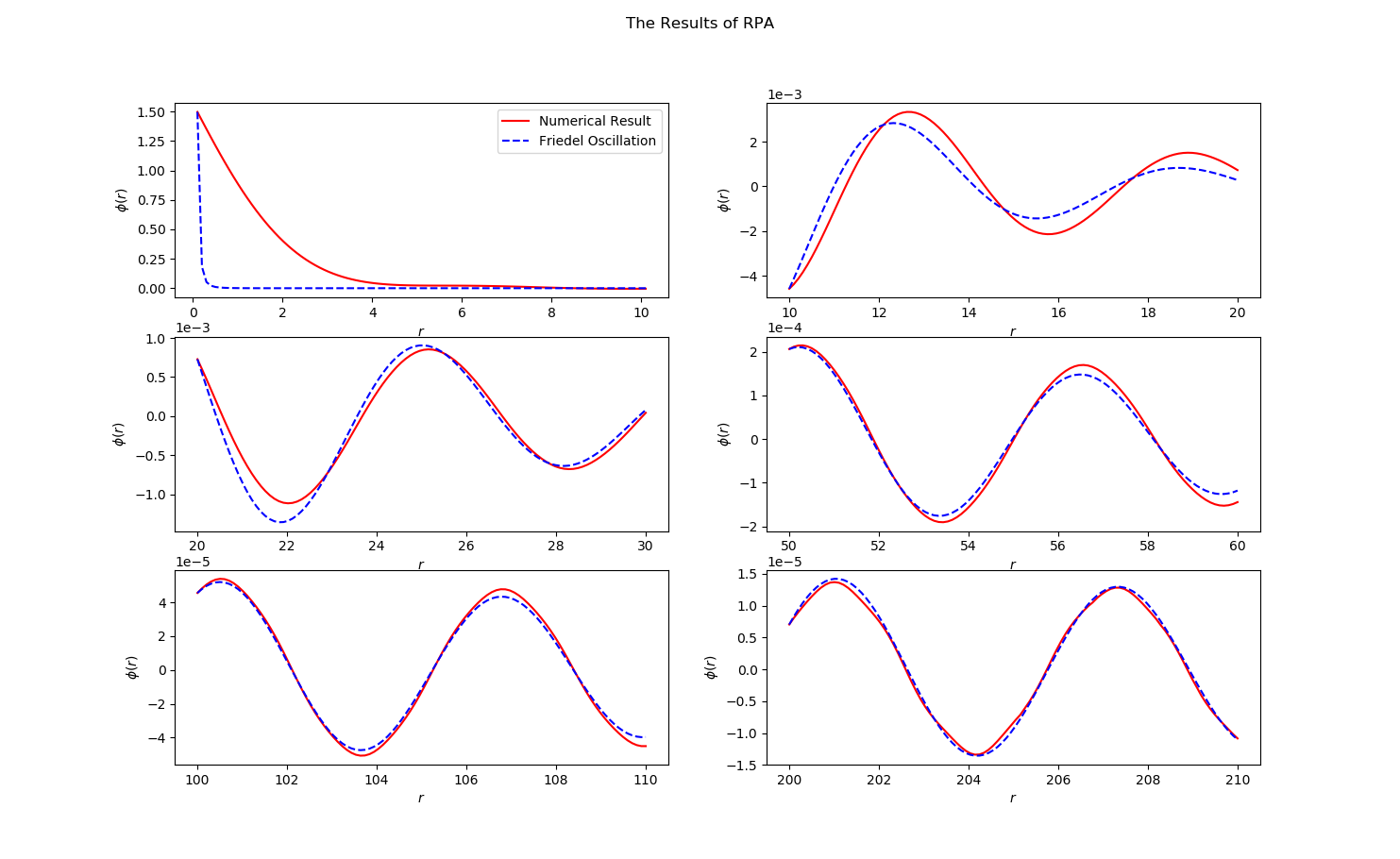
可以看出, Friedel Oscillations 的结果在 $r$ 较大时的结果比较好.
参考文献
Friedel Oscillation 的原始文献 the shielding of a fixed charge in a high-density electron gas http://www.doc88.com/p-9512851691956.html
Wolfgang Nolting, Fundamentals of Many-body Physics
致谢
感谢导师 Ran Qi 的指导
感谢 Fan Yang 师兄的讨论