Rabi's Formula (update 15/Apr/2020)
Statement of the Problem
二能级系统的 Hamiltonian
$$\begin{align*} H = H_0 + V \end{align*}$$$H_0$ 的两个本征态为 $|1\rangle ,\,|2\rangle$ . 在这两个 本征态组成的 Hilbert 空间写出 Hamiltonian 的矩阵形式
$$\begin{align*} H = \pmatrix{E_1 & 0 \\0 & E_2} + \pmatrix{0 & V_{12} \\ V_{21} & 0} \end{align*}$$其中 $V_{12}=V_{21}^{*} = \gamma e^{\mathrm{i}\omega t}$ 在 Dirac Representation 中, $t$ 时刻处于态 $|\psi(t) \rangle_D = c_1(t) |1\rangle +c_2(t)|2\rangle$ ,且 $c_1(0) = 1, \quad c_2(0) = 0$
其中$|\psi(t) \rangle_D = e^{-\frac{1}{\mathrm{i}\hbar}H_0t}|\psi(t)\rangle$ , 求 $c_1(t),\quad c_2(t)$
Dirac Representation
$$\begin{align*} \mathrm{i}\hbar\frac{\partial}{\partial t}c_1(t) &= \mathrm{i}\hbar \frac{\partial}{\partial t} \langle 1 |\psi(t)\rangle_D \\ &= \langle 1|\cdot\mathrm{i}\hbar \frac{\partial}{\partial t} |\psi(t)\rangle_D \end{align*}$$而 Dirac Representation 中的运动方程
$$\begin{align*} \mathrm{i}\hbar \frac{\partial}{\partial t} |\psi(t)\rangle _D = V_D |\psi(t)\rangle_D \end{align*}$$所以
$$\begin{align*} \mathrm{i}\hbar\frac{\partial}{\partial t}c_1(t) &= \langle 1 |V_D |\psi(t)\rangle_D \end{align*}$$插入一组完备基
$$\begin{align*} \mathrm{i}\hbar\frac{\partial}{\partial t}c_1(t) =& \langle 1 |V_D \cdot \left( |1 \rangle\langle 1| + |2\rangle\langle 2| \right) \cdot |\psi(t)\rangle_D \\ =&e^{\frac{\mathrm{i}}{\hbar}(E_1-E_1)t}V_{11} c_1(t) +e^{\frac{\mathrm{i}}{\hbar}(E_1-E_2)t}V_{12} c_2(t) \end{align*}$$其中
$$\begin{align*} V_{11}=& \langle 1| V_D |1\rangle \\ V_{12}=& \langle 1 |V_D | 2\rangle \end{align*}$$同理可得 $c_2(t)$ 的微分方程
若记 $(E_n-E_m)/\hbar =\omega_{nm}$ , 则最终得到一个微分方程组
$$\begin{align*} \mathrm{i}\hbar\dot{c}_1 = V_{11} c_1 + e^{\mathrm{i}\omega_{12}t}V_{12} c_2 \\ \mathrm{i}\hbar \dot{c}_2 =e^{\mathrm{i}\omega_{21}t} V_{21} c_1 + V_{22} c_2 \end{align*}$$求解微分方程组
化简
对于这个问题, $V_{11} = V_{22} 0$ , $V_{12}V_{21}^{*} = \gamma e^{\mathrm{i}\omega t}$ ,所以
即
$$\begin{align*} \mathrm{i}\hbar\dot{c}_1 =& \gamma e^{\mathrm{i}(\omega-\omega_{21})t} c_2 \tag{1}\\ \mathrm{i}\hbar\dot{c}_2 =&\gamma e^{-\mathrm{i}(\omega-\omega_{21})t} c_1\tag{2} \end{align*}$$求解
$(2)$ 移项得
$$\begin{align*} c_1 =\frac{\mathrm{i}\hbar}{\gamma}e^{\mathrm{i}(\omega-\omega_{21})t} \dot{c}_2 \end{align*}$$两边对 $t$ 求导
$$\begin{align*} \dot{c}_1 =\frac{\mathrm{i}\hbar}{\gamma}e^{\mathrm{i}(\omega-\omega_{21})t} [\mathrm{i}(\omega-\omega_{21})\dot{c}_2 +\ddot{c}_2] \tag{3} \end{align*}$$将 $(1)$ 式代入 $(3)$ 式得
$$\begin{align*} \frac{\gamma}{\mathrm{i}\hbar} e^{\mathrm{i}(\omega-\omega_{21})t} c_2 =\frac{\mathrm{i}\hbar}{\gamma}e^{\mathrm{i}(\omega-\omega_{21})} [\mathrm{i}(\omega-\omega_{21})\dot{c}_2 +\ddot{c}_2] \end{align*}$$整理成标准形式
$$\begin{align*} \ddot{c}_2 + \mathrm{i}(\omega-\omega_{21})\dot{c}_2 + \frac{\gamma^2}{\hbar^2}c_2 =0 \end{align*}$$其解的形式为
$$\begin{align*} c_2(t) = e^{-\frac{\mathrm{i}}{2}(\omega-\omega_{21})t} \left(Ae^{\mathrm{i}\Omega t} + B e^{-\mathrm{i}\Omega t} \right) \tag{4} \end{align*}$$其中
$$\begin{align*} \Omega = \sqrt{\frac{(\omega-\omega_{21})^2}{4}+\frac{\gamma^2}{\hbar^2}} \end{align*}$$$(4)$ 式代入 $(2)$ 式得
$$\begin{align*} c_1(t)=\frac{\mathrm{i}\hbar}{\gamma}e^{\mathrm{i}(\omega-\omega_{21})t} \cdot e^{-\frac{\mathrm{i}}{2}(\omega-\omega_{21})t}\left[ -\frac{i}{2}(\omega-\omega_{21})\left(Ae^{\mathrm{i}\Omega t} + B e^{-\mathrm{i}\Omega t} \right) + \mathrm{i}\Omega\left(Ae^{\mathrm{i}\Omega t} - B e^{-\mathrm{i}\Omega t} \right)\right]\tag{5} \end{align*}$$将初值条件 $c_1(0) = 1, \quad c_2(0) = 0$ 代入 $(4), (5)$ 式得
$$\begin{align*} A+B =& 0 \\ \frac{\mathrm{i}\hbar}{\gamma}\cdot \mathrm{i}\Omega(A-B) =&1 \end{align*}$$解得
$$\begin{align*} A =& -\frac{\gamma}{2\hbar\Omega} \\ B =& \frac{\gamma}{2\hbar\Omega} \end{align*}$$将系数 $A,\,B$ 的结果代入 $(4) ,\,(5)$ 式得
$$\begin{align*} c_2(t) =& -\frac{\mathrm{i}\gamma}{\hbar\Omega} e^{-\frac{\mathrm{i}}{2}(\omega-\omega_{21})t} \sin(\Omega t) \\ c_1(t) =&-\frac{\mathrm{i}}{2\Omega}(\omega-\omega_{21})e^{\frac{\mathrm{i}}{2}(\omega-\omega_{21})t}\sin (\Omega t) + e^{\frac{\mathrm{i}}{2}(\omega-\omega_{21})t}\cos (\Omega t) \end{align*}$$取模方有
$$\begin{align*} |c_2(t)|^2 = \frac{1}{1+\frac{\hbar^2(\omega-\omega_{21})^2}{4\gamma^2}}\sin^2\left( \Omega t \right) \end{align*}$$Results
code
import numpy as np
from matplotlib import pyplot as plt
from matplotlib import animation
N = 1000
gamma = 1
t = np.linspace(0,16,N)
def c2(omega):
Omega = np.sqrt( (omega-1)**2/4 + gamma )
c2 = 1/( 1+(omega-1)**2/(4*gamma**2) ) \
*np.sin(Omega*t)**2
ax.set_xticks([np.pi/Omega, 2*np.pi/Omega, \
3*np.pi/Omega, 4*np.pi/Omega, \
5*np.pi/Omega])
ax.set_xlim(0,4*np.pi/Omega)
return c2
fig, ax = plt.subplots()
line, = ax.plot(t,c2(1))
#ax3 = fig.add_axes([0.1, 0.1, 0.8, 0.8])
def init():
line.set_ydata(c2(1))
return line
def animata(i):
line.set_ydata(c2(1+.01*i))
# ax.text(1+0.1*i,1,'x')
return line
ani = animation.FuncAnimation(fig=fig, func=animata, \
frames=400, interval=20)
ax.set_xlabel('$t$')
ax.set_ylabel('$|c_2(t)|^2$')
ax.set_title('Plot of $|c_2(t)|^2$ at $\omega = \omega_{21}$ to $\omega =5 \omega_{21}$')
ax.set_yticks([0,0.2,0.5,1])
ax.set_xticklabels(['$\pi/\Omega$', '$2\pi/\Omega$', \
'$3\pi/\Omega$', '$4\pi/\Omega$', \
'$5\pi/\Omega$'])
ani.save('fig.gif',writer='imagemagick')
plt.show()
figure
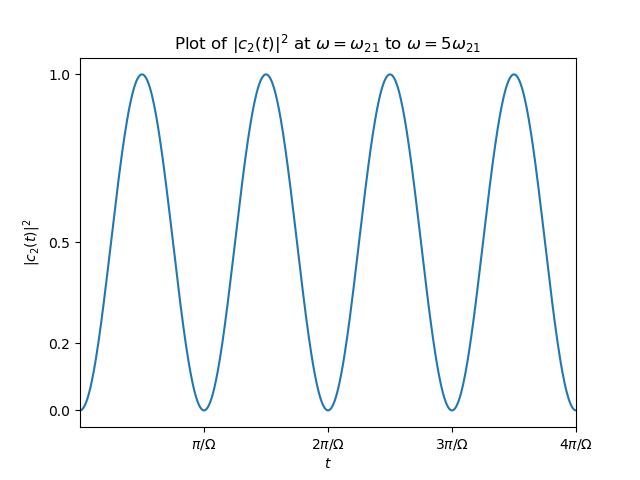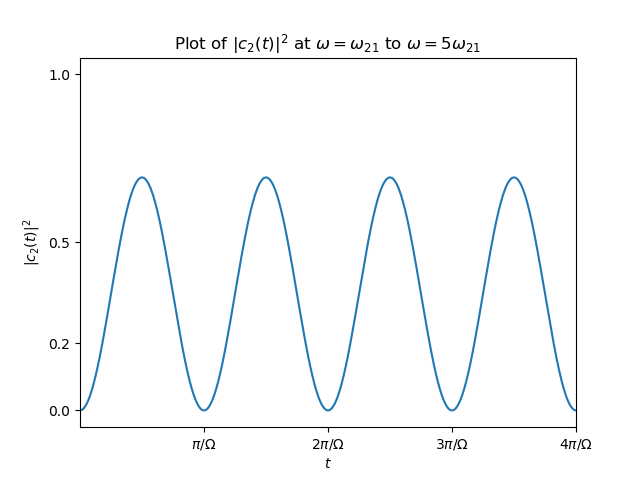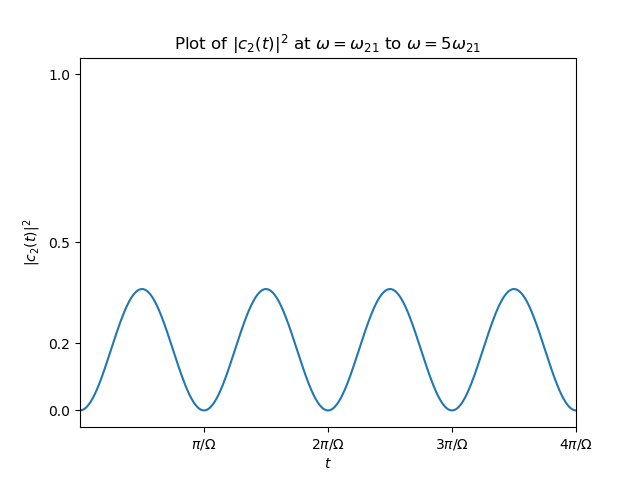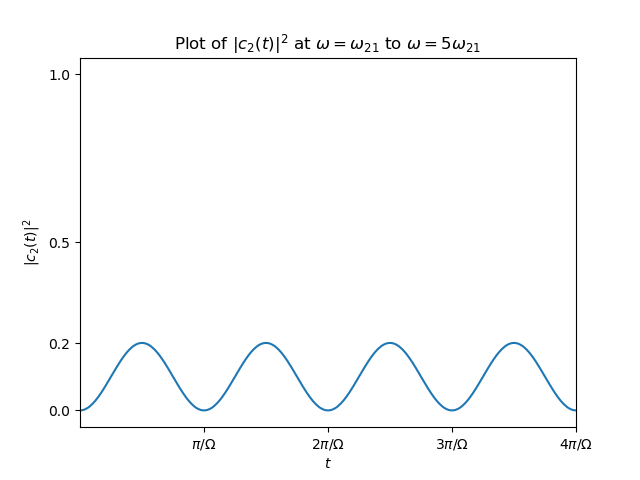
./2019-03-06-physics-RabiFormula/fig.mp4
总结
如果取 $\hbar = 1$ , 记 detuning $\Delta = \omega-\omega_{21}$ , 那么对于一个二能级系统的(含时) 微扰
$$\begin{align} V_{12} = \gamma e^{\mathrm{i}\omega t} \end{align}$$在 Dirac 表象(态矢中去除了 $H_0$ 的演化)中
$$\begin{align} c_2(t) =& -\frac{\mathrm{i}\gamma}{\Omega} e^{-\frac{\mathrm{i}}{2}\Delta t} \sin(\Omega t) \end{align}$$ $$\begin{align} |c_2(t)|^2 = \left(\frac{\gamma}{\Omega}\right)^2\sin^2\left( \Omega t \right) \end{align}$$其中 Rabi frequency $\Omega$ ( $|c_2(t)|^2$ 以 $2\Omega$ 为角频率振荡) 为
$$\begin{align} 2\Omega = \sqrt{\Delta^2+(2\gamma)^2} \end{align}$$可以看出, detuning 越大, Rabi frequency 越大, $|c_2(t)|^2$ 振幅越小.这是当然的, 失 谐大了, 耦合就弱, 因为初态取了 $c_2(0)=0$ .
Reference
http://farside.ph.utexas.edu/teaching/qmech/Quantum/node113.html
J. J. Sakurai, Jim Napolitano, Modern Quantum Mechanics 2nd