从冰上的水 - Classical Forced Oscillator 经典受迫振动

model

\begin{array}{r} \ddot{x} = - ω^{2} x + F (t) \end{array}

In Landau's book, the solution(non-resoance) is

\begin{array}{r} ξ (t) = e^{i ω t} \int_{0}^{t} d t^{'} \cdot F (t^{'}) e^{- i ω t^{'}} \end{array}

\begin{array}{r} x (t) = A \sin (ω t) + B \cos (ω t) + \frac{Im [ξ (t)]}{ω} \end{array}

where

\begin{aligned} B = & x (t) \\ A = & \frac{1}{ω} (\dot{x} (0) - \frac{\dot{ξ} (0)}{ω}) \end{aligned}

solve by Fourier transform

For

\begin{array}{r} F (t) = f_{γ} \cos (γ t) \end{array}

it is easy get

\begin{array}{r} x_{γ} (t) = A \cos (ω t + ϕ) + \frac{f_{γ}}{ω^{2} - γ^{2}} \cos (γ t) \end{array}

Similar for

\begin{array}{r} F (t) = f_{γ} \sin (γ t) \end{array}

For non-resonance case, it is easy get

\begin{array}{r} x_{γ} (t) = A \cos (ω t + ϕ) + \frac{f_{γ}}{ω^{2} - γ^{2}} \sin (γ t) \end{array}

So, for

\begin{array}{r} F (t) = \frac{1}{\sqrt{2 π}} \int_{- \infty}^{\infty} \tilde{F} (γ) e^{i γ t} d γ \end{array}

where

\begin{array}{r} \tilde{F} (γ) = \frac{1}{\sqrt{2 π}} \int_{- \infty}^{\infty} F (t) e^{- i (γ + i 0^{+}) t} d t \end{array}

(where $i 0^{+}$ is for the Fourier transforms such as sine function) we have

\begin{array}{r} x (t) = A \cos (ω t + ϕ) + x_{1} (t) \end{array}

where

\begin{array}{r} x_{1} (t) = P \frac{1}{\sqrt{2 π}} \int_{- \infty}^{\infty} d γ \cdot \frac{\tilde{F} (γ)}{ω^{2} - γ} e^{i γ t} \end{array}

becasue we only consider the non-resoance case, the principal value $P$ is added. We can use the identity(Sokhotski–Plemelj theorem)

\begin{array}{r} \int_{0}^{\infty} d s \cdot e^{- i (ω + i 0^{+}) s} = \frac{1}{i (ω + i 0^{+})} = π δ (ω) - i P \frac{1}{ω} \end{array}

get a more physical form

\begin{aligned} x_{1} (t) = & \frac{1}{\sqrt{2 π}} P \int_{- \infty}^{\infty} d γ \cdot \frac{1}{2 ω} [\frac{1}{ω - γ} + \frac{1}{ω + γ}] \tilde{F} (γ) e^{i γ t} \\ = & \frac{1}{2 ω} (- 1) Im {\int_{0}^{\infty} d s \cdot e^{- i (ω + i 0^{+}) s} [F (t + s) + F (t - s)]} \end{aligned}

We also add $i 0^{+}$ here for a possible $lim_{t \to \infty} F (t) \neq 0$ , such as $F (t) = \sin (t)$ . We can also substract a homogeous solution from it to get the solution in Landau's book

\begin{array}{r} x_{1} (t) + \frac{1}{2 ω} Im {e^{i ω t} [\int_{0}^{\infty} e^{- i (ω + i 0^{+}) s} F (s) d s - \int_{- \infty}^{0} e^{- i (ω + i 0^{+}) s} F (s) d s]} = \frac{Im [ξ (t)]}{ω} \end{array}

All these are check by the following numerical code

code

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
from scipy.integrate import quad


def quad_c(func, *args, **kwargs):
    re = quad(lambda x: func(x).real, *args, **kwargs)
    im = quad(lambda x: func(x).imag, *args, **kwargs)
    return re[0]+1j*im[0], re[1]+1j*im[1]


def ftrans(func, x):
    res = quad_c(func, 0, np.inf, weight='cos', wvar=x)[0]
    res += 1j*quad(func, 0, np.inf, weight='sin', wvar=x)[0]
    res += quad(func, -np.inf, 0, weight='cos', wvar=x)[0]
    res += 1j*quad(func, -np.inf, 0, weight='sin', wvar=x)[0]
    return res/np.sqrt(2*np.pi)


class Oscillator:
    def __init__(self, w, Ft, x0, v0):
        """
        dx^2/dt^2 + w^2 = Ft
        w: oemga
        Ft: function of t
        x0: intial position
        v0: intial dx/dt, volecity
        """
        self.w = w
        self.Ft = Ft
        self.x0 = x0
        self.v0 = v0

    def dX_dt(self, X, t):
        return [X[1], -self.w**2*X[0] + self.Ft(t)]

    def xi_im_landau(self, t):
        """
        Imaginary part of Landau (22.10) with out xi_0
        """
        xil = - quad(self.Ft, 0, t,
                     weight='sin', wvar=self.w)[0] * np.cos(self.w*t)
        xil += quad(self.Ft, 0, t,
                    weight='cos', wvar=self.w)[0] * np.sin(self.w*t)
        return xil

    def X_t_ana(self, t, ts):
        xt = self.xi_im_landau(t) / self.w

        xt += np.cos(self.w*t) * self.x0

        dxi_dt0 = self.xi_im_landau(ts[1]) - self.xi_im_landau(ts[0])
        dxi_dt0 /= ts[1] - ts[0]

        xt += np.sin(self.w*t) * (self.v0 - dxi_dt0/self.w) / self.w
        return xt

    def X_t_ana_FT(self, t):
        xt = quad(lambda s: (self.Ft(t+s) + self.Ft(t-s)), 0, np.inf,
                  weight='sin', wvar=self.w)[0]
        xt /= (2*self.w)

        cor = np.sin(self.w*t) * quad(self.Ft, 0, np.inf,
                                      weight='cos', wvar=self.w)[0]
        cor -= np.cos(self.w*t) * quad(self.Ft, 0, np.inf,
                                       weight='sin', wvar=self.w)[0]
        cor -= np.sin(self.w*t) * quad(self.Ft, -np.inf, 0,
                                       weight='cos', wvar=self.w)[0]
        cor += np.cos(self.w*t) * quad(self.Ft, -np.inf, 0, weight='sin',
                                       wvar=self.w)[0]

        xt += cor/(2*self.w)
        xt += np.cos(self.w*t) * self.x0

        dxi_dt0 = self.xi_im_landau(ts[1]) - self.xi_im_landau(ts[0])
        dxi_dt0 /= ts[1] - ts[0]

        xt += np.sin(self.w*t) * (self.v0 - dxi_dt0/self.w) / self.w
        return xt

    def Xt_ode(self, ts):
        Xs = odeint(self.dX_dt, [self.x0, self.v0], ts)
        return Xs


osc = Oscillator(w=.5, Ft=lambda t: 5*np.exp(-(t-10)**2), x0=.7, v0=.5)
ts = np.linspace(0, 30, 300)
plt.plot(ts, [osc.X_t_ana_FT(ti) for ti in ts], 'ro', mfc='None', ms=10,
         label='Fourier')
plt.plot(ts, osc.Xt_ode(ts)[:, 0], 'bx', label="Numerically solve ODE")
plt.plot(ts, [osc.X_t_ana(ti, ts) for ti in ts], 'g', label='Analytic', lw=2)
plt.xlabel('t')
plt.legend()
plt.savefig('osc.png', transparent=True)
plt.show()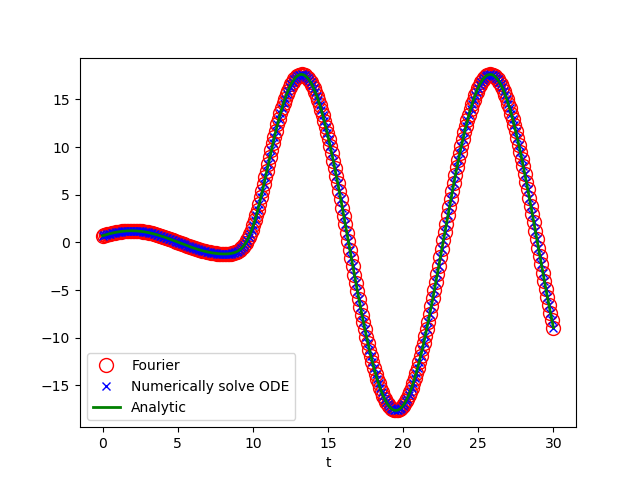

osc.py

osc_fig

Caution

scipy.integrate.quad method gives a wrong result when use weight and infinity integral range. The following integral are not converge, but the code give a result without waring or error. Why? if I have time, ...

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad


def quad_recorded(func, *args, **kwargs):
    """
    use scipy.integrate.quad, but return the results with additional
    information "nc" and "vc"
    Returns:
        inte_res: the return of scipy.integrate.quad
              nc: the points calculated
              vc: the calculated functiona values
    """
    def func_recorded(x, node_container, value_container):
        res = func(x)
        node_container.append(x)
        value_container.append(res)
        return res
    nc = []
    vc = []
    inte_res = quad(lambda x: func_recorded(x, node_container=nc,
                                            value_container=vc),
                    *args, **kwargs)
    idx = np.argsort(np.array(nc))
    nc = np.array(nc)[idx].tolist()
    vc = np.array(vc)[idx].tolist()
    return inte_res, nc, vc


r, nc, vc = quad_recorded(np.sin, 0, np.inf, weight='sin', wvar=0.2)
plt.plot(nc, vc, '-x')
plt.savefig('caution.png', transparent=True)
print(r)

  >>> (2.4313884239290928e-14, 2.0748702051907655e-10)

caution.py

Reference

Mechanics, Third Edition: Volume 1 (Course of Theoretical Physics)
Wikipedia: Sokhotski–Plemelj theorem