Scattering Length
Schrodinger EQ
Equation
两体运动的相对运动的 Schrodinger 方程为
$$\begin{align} \left[ -\frac{\hbar^2}{2\mu}\nabla^2 + V(r) -E\right]\psi = 0 \end{align}$$变形为
$$\begin{align} \nabla^2 \psi = \left[ \frac{2\mu}{\hbar^2} V(r) - k^2 \right]\psi \end{align}$$其中 $k^2 = E/\frac{\hbar^2}{2\mu}$ . 写出 $\nabla^2$ 在球 坐标系中的形式, 方程变为
$$\begin{align} \left[\frac{1}{r^2}\frac{\partial}{\partial r}r^2 \frac{\partial}{\partial r} + \frac{1}{r^2 \sin \theta}\frac{\partial}{\partial \theta}\sin \theta \frac{\partial}{\partial \theta} + \frac{1}{r^2\sin^2 \theta}\frac{\partial^2}{\partial\varphi^2} \right] \psi = \left[ \frac{2\mu}{\hbar^2} V(r) - k^2 \right]\psi \end{align}$$分离变量
分离变量, 令
$$\begin{align} \psi(r,\theta,\phi) = R(r)\Theta(\theta)\Phi(\phi) \end{align}$$代回方程, 并且两边同时除以 $R(r)\Theta(\theta)\Phi(\varphi)$ 可得
$$\begin{align} \frac{1}{R}\frac{1}{r^2}\frac{\mathrm{d}}{\mathrm{d} r}r^2 \frac{\mathrm{d}}{\mathrm{d} r} R+ \frac{1}{\Theta}\frac{1}{r^2 \sin \theta}\frac{\mathrm{d}}{\mathrm{d} \theta}\sin \theta \frac{\mathrm{d}}{\mathrm{d} \theta}\Theta +\frac{1}{\Phi} \frac{1}{r^2\sin^2 \theta}\frac{\mathrm{d}^2}{\mathrm{d}\varphi^2}\Phi = \frac{2\mu}{\hbar^2} V(r) - k^2 \end{align}$$所有含有 $\varphi$ 的项都在方程左边第三项, 与 $r,\theta$ 没有耦合, 所以 它一定是一个常数. 因为其它的项中都与 $\theta$ 无关, $\theta$ 改变时其它 项保持不变. 记这个常数为 $-m^2$ 即
$$\begin{align} \frac{1}{\Phi}\frac{\mathrm{d}^2}{\mathrm{d}\varphi^2}\Phi = -m^2 \end{align}$$将它代回原方程, 原方程变为
$$\begin{align} \frac{1}{R}\frac{1}{r^2}\frac{\mathrm{d}}{\mathrm{d} r}r^2 \frac{\mathrm{d}}{\mathrm{d} r} R+ \frac{1}{\Theta}\frac{1}{r^2 \sin \theta}\frac{\mathrm{d}}{\mathrm{d} \theta}\sin \theta \frac{\mathrm{d}}{\mathrm{d} \theta}\Theta - \frac{m^2}{r^2\sin^2 \theta} = \frac{2\mu}{\hbar^2} V(r) - k^2 \end{align}$$$\theta$ 和 $r$ 也没有耦合, 同理可以把与 $\theta$ 有关的项单拎出来, 是一个常数, 记为 $-\lambda$ ,即
$$\begin{align} \frac{1}{\Theta}\frac{1}{ \sin \theta}\frac{\mathrm{d}}{\mathrm{d} \theta}\sin \theta \frac{\mathrm{d}}{\mathrm{d} \theta}\Theta - \frac{m^2}{\sin^2 \theta} = -\lambda \end{align}$$上述关于 $\theta$ 的方程的解是连带 Legendre 多项式 $P_l^m(\cos\theta)$, 本征值 $\lambda$ 只能取值为 $l(l+1)$ , $l$ 是个 整数. 如果 $m=0$ ,解则是一个 Legendre 多项式. Supplementary 中用 Frobenius 方法(即级数解法) 求解 $m= 0$ 的情况.
剩下的只有 $r$ 的方程为
$$\begin{align} \frac{1}{R}\frac{1}{r^2}\frac{\mathrm{d}}{\mathrm{d} r}r^2 \frac{\mathrm{d}}{\mathrm{d} r} R = \frac{2\mu}{\hbar^2} V(r) - k^2 +\frac{l(l + 1)}{r^2} \end{align}$$即
$$\begin{align} \frac{1}{r^2}\frac{\mathrm{d}}{\mathrm{d} r}r^2 \frac{\mathrm{d}}{\mathrm{d} r} R -\left[ \frac{2\mu}{\hbar^2} V(r) - k^2 +\frac{l(l + 1)}{r^2}\right]R =0 \end{align}$$它的一般解的形式是球 Bessel 函数.
$m0$ and $l0$
由于散射势 $V(r)$ 是球对称的, 那么其波函数应该沿入射方向是轴对称的. 选
取入射方程是 $z$ 方向, 那么角动量在 $z$ 方向上动量为 $0$ (可与经典
散射类比). 也就是说 $m 0$ . 在 $m0$ 的情况下, 本征波函数的形式为
对于径向关于 $r$ 方程可以做变量代换
$$\begin{align} R_{kl}(r) = \frac{\chi_{kl}(r)}{kr} \end{align}$$设入射波函数为 $\Psi$ ,它可以是不同分波的本征波函数的任意叠加, 即
$$\begin{align} \Psi = \sum_{l = 0}^{+\infty} \frac{\chi_{kl}(r)}{kr}P_l(\cos\theta) \end{align}$$径向方程为
$$\begin{align} \frac{\mathrm{d}^2}{\mathrm{d}r^2}\chi -\left[ \frac{2\mu}{\hbar^2} V(r) - k^2 +\frac{l(l + 1)}{r^2}\right]\chi =0 \end{align}$$以下只关心 s 波散射, 也就是 $l=0$ ,方程化为
$$\begin{align} \frac{\mathrm{d}^2}{\mathrm{d}r^2}\chi =\left[ \frac{2\mu}{\hbar^2} V(r) - k^2 \right]\chi \end{align}$$Scattering Length
考虑有限力程的散射, 也就是 $V(r>r_0)=0$ .因此, 对于力程之外, 方程化为
$$\begin{align} \frac{\mathrm{d}^2}{\mathrm{d}r^2}\chi =- k^2 \chi \end{align}$$其中 $k^2 = E/\frac{\hbar^2}{2\mu}$ ,很明显, $E>0$ , 是一个散射 态. 容易解得
$$\begin{align} \chi_k(r>r_0) = A \sin (kr +\delta_{k}) \end{align}$$在 $r=r_0$ 处的 $r$ 连接条件为
$$\begin{align} \left.\frac{\chi'(r>r_0)}{\chi(r>r_0)}\right|_{r=r_0} = \frac{k\cos(kr_0 +\delta_k)}{\sin(kr_0\delta_{k})} = \left.\frac{\chi'(r < r_0)}{\chi(r < r_0)}\right|_{r=r_0} \end{align}$$低能散射下, $kr_0\approx 0$ ,取 $kr_0$ 的 Leading order,
$$\begin{align} \left.\frac{\chi'(r>r_0)}{\chi(r>r_0)}\right|_{r=r_0} \approx \frac{k}{\tan \delta_k} \end{align}$$用以下极限定义散射长度 $a_s$
$$\begin{align} \lim_{k\to 0}\frac{k}{\tan \delta_k} = -\frac{1}{a_s} \end{align}$$取极限时, 相当于极限的分子分母的 Leading order 系数之比. 如果取到 更高阶, 第二阶为 effective range $r_{\mathrm{eff}}$
$$\begin{align} \frac{k}{\tan \delta_k} = -\frac{1}{a_s} + \frac{1}{2} ** r_{\mathrm{eff}}k^2 \end{align}$$低能散射时, 如果波函数也只取到 $k$ 的 Leading order
$$\begin{align} \chi(r>r_0) \propto& \sin(kr+\delta_k) \approx \sin \delta_k + kr\cos \delta_k \\ &\propto 1+ \frac{k}{\tan\delta_k}r = 1-\frac{r}{a_s} \end{align}$$Square Well and Shallow Bound State
求有限深球方势阱的散射长度随势阱深度的变化, 以及束缚态能量.
球方势阱
$$\begin{align*} V(r) = \left\{ \begin{aligned} 0 & , r > r_0 \\ -V_0 & , r < r_0 \end{aligned} \right. \end{align*}$$定态 Schrodinger 方程解的形式为
$$\begin{align*} \psi(r,\theta,\varphi) = \frac{\chi _l(r)}{r}Y_l^m(\theta,\varphi) \end{align*}$$对于 $l=0$ 的 s 分波, 其径向波函数满足
$$\begin{align*} \frac{\mathrm{d}^2}{\mathrm{d}r^2}\chi_r = -\frac{2\mu}{\hbar^2}[E-V(r)]\chi(r) \end{align*}$$对于 $E>0$ 的散射态, 当 $r > r_0$ 时的径向解为
$$\begin{align*} \chi(r>r_0)\propto \sin(k r + \delta_k) \end{align*}$$其中 $k = \frac{\sqrt{2\mu E}}{\hbar}$ . 当 $r < r_0$ 时
$$\begin{align*} \chi(r < r_0) \propto \sin(\kappa r) \end{align*}$$其中 $\kappa = \frac{\sqrt{2\mu(E+V_0)}}{\hbar}$ . 在 $r=r_0$ 处的连接条件为
$$\begin{align*} \left.\frac{\chi'(r>r_0)}{\chi(r > r_0)}\right|_{r=r_0} = k \frac{\cos(kr_0+\delta_k)}{\sin(kr_0+\delta_k)} = \left.\frac{\chi'(r < r_0)}{\chi(r < r_0)}\right|_{r=r_0} = \frac{\kappa}{\tan(\kappa r_0)} \end{align*}$$由上式可解得
$$\begin{align*} \frac{\tan(\delta_k)}{k} = \frac{k \tan(\kappa r_0)\cos(kr_0)-\kappa \sin(kr_0)} {\kappa k + k \tan(\kappa r_0)\sin(kr_0)} \end{align*}$$由散射长度的定义可得
$$\begin{align*} -\frac{1}{a_s} =& \lim_{k\to0} \frac{k}{\tan(\delta_k)} \\ =&\lim_{k\to0}\frac{\kappa k + k \tan(\kappa r_0)\sin(kr_0)}{k \tan(\kappa r_0)\cos(kr_0)-\kappa \sin(kr_0)} \\ =&\frac{1}{\frac{\tan(\kappa_0 r_0)}{\kappa_0}-r_0} \end{align*}$$ 其中 $\kappa_0 \kappa|_{k0} = \frac{\sqrt{2\mu V_0}}{\hbar}$ . 所以
无量纲化
$$\begin{align*} \tilde{a}_s = 1 - \frac{\tan(\sqrt{\tilde{V}_0})}{\sqrt{\tilde{V}_0}} \end{align*}$$其中 $\tilde{a}_s = \frac{a_s}{r_0}$ , $\tilde{V}_0 = \frac{V_0}{\hbar^2/(2\mu r_0^2)}$ . 对于 $-V_0 < E_b < 0$ 的束缚态
$$\begin{align*} \begin{cases} \chi(r > r_0)\propto& e^{-k'r} \\ \chi(r < r_0)\propto& \sin (\kappa r) \end{cases} \end{align*}$$其中 $k' = \frac{\sqrt{2\mu(-E_b)}}{\hbar}$ . 类似地, 由 $r = r_0$ 处的连接条件得
$$\begin{align*} -k' = \frac{\kappa}{\tan(\kappa r_0)} \end{align*}$$无量纲化的结果为
$$\begin{align*} -\sqrt{-\tilde{E}_b} = \frac{\sqrt{\tilde{E}_b+\tilde{V}_0}}{\tan(\sqrt{\tilde{E}_b+\tilde{V}_0})} \end{align*}$$其中 $\tilde{E}_b = \frac{E_b}{\hbar^2/(2\mu r_0^2)}$ . $k'$ 在 $E_b$ 很小下的行为
$$\begin{align*} k'= \frac{\sqrt{2\mu(-E_b)}}{\hbar}\sim-\frac{\kappa_0}{\tan(\kappa r_0)} = \frac{1}{a_s - r_0} \end{align*}$$可以看出, 只有当 $a_s>0$ 时才可能有解. 且在 $a_s\gg r_0$ 时有
$$\begin{align*} E_b \sim -\frac{\hbar^2}{2\mu a_s^2} \end{align*}$$无量纲化的结果为
$$\begin{align*} \tilde{E}_b \sim -\frac{1}{\tilde{a}_s^2} \end{align*}$$散射长度随势阱深度的变化, 以及低能束缚态在 $a_s\gg r_0$ 时的渐进行为如图所示
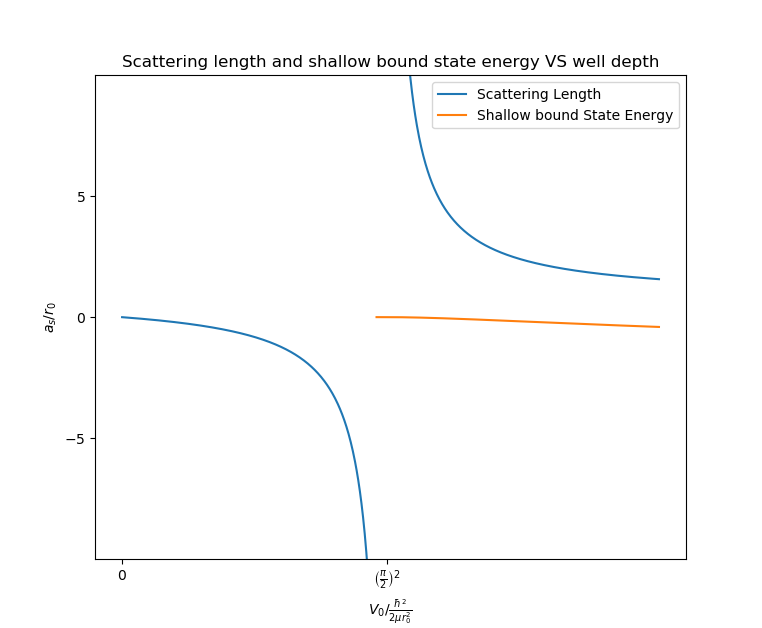
file:./2019-04-03-physics-两体散射/Figure_1.eps
file:./2019-04-03-physics-两体散射/scatterlength.py
Partial-Wave Expansion
Expansion of plane waves in spherical harmonics
为讨论分波展开做准备, 先讨论将平面波用 Legendre 函数展开.
考虑沿 $\vec{k}$ 方向传播的平面波, 其波函数为(未归一的) $e^{\mathrm{i}\vec{k}\cdot \vec{r}} = e^{\mathrm{i}kr\cos\theta}$ . 其中 $r = |\vec{r}|$ .如果选取平面波的 传播方向为 $z$ 方向, 即 $\vec{k} = k \hat{z}$ , 那么平面波就 可以写为 $e^{\mathrm{i}kz}$ .
前面已经讨论过, 对于有心力场的 Schrodinger 方程, 其角向 的解是连带 Legendre 函数. 我们考虑的平面波取了传播方向为 $z$ 方向, 那么角动量的 $z$ 分量就是零, 这时, 连带 Legendre 函数中 $m=0$ ,角向解就变为 Legendre 方程.
Legendre 多项 $P_l(\cos\theta)$ 式在 $\cos\theta\in [-1,1]$ 上 构成一组完备正交基, 正交完备关系如下
$$\begin{align} \int_{-1}^1 P_l(\cos\theta) P_{l'}(\cos\theta) \cdot \mathrm{d}\cos\theta = \delta_{l,l'}\cdot\frac{2}{2l+1} \end{align}$$将平面波用 Legendre 多项式展开
$$\begin{align} e^{\mathrm{i}kr\cos\theta} = \sum_{l=0}^{\infty} C_l\cdot P_l(\cos\theta) \end{align}$$将等式两边乘上 $P_{l'}(\cos\theta)$ 再积分, 利用正交归一性可求得 展开系数 $C_l$
$$\begin{align} C_l = \frac{2l+1}{2}\int_{-1}^1 e^{\mathrm{i}kr\cos\theta} P_l(\cos\theta) \cdot \mathrm{d}\cos\theta \end{align}$$我们需要的是在 $r\to\infty$ 时的结果, 因此只需要展开系数 $C_l$ 在 $r\to\infty$ 时的渐进结果, 也就是只保留 Leading order . 对上式中的积分用分部 积分法
$$\begin{align*} & \int_{-1}^1 e^{\mathrm{i}krt} P_l(t) \cdot \mathrm{d}t \\ =&\frac{1}{\mathrm{i}kr} \int_{-1}^1 P_l(t) \cdot \mathrm{d}e^{\mathrm{i}krt} \\ =& \left.\frac{1}{\mathrm{i}kr}e^{\mathrm{i}krt} P_l(t)\right|_{-1}^1 -\frac{1}{\mathrm{i}kr}\int_{-1}^1 e^{\mathrm{i}krt} P'_l(t) \cdot \mathrm{d}t \\ =& \left.\frac{1}{\mathrm{i}kr}e^{\mathrm{i}krt} P_l(t)\right|_{-1}^1 +\frac{1}{(kr)^2}\left[ \left.e^{\mathrm{i}krt} P'_l(t)\right|_{-1}^1 -\int_{-1}^1 e^{\mathrm{i}krt} P''_l(t) \cdot \mathrm{d}t \right]\\ =& \frac{1}{\mathrm{i}kr}\left( e^{\mathrm{i}kr}-e^{-\mathrm{i}kr} e^{\mathrm{i}\pi l} \right) + \mathcal{O}\left(\frac{1}{(kr)^2}\right) \\ =& \frac{2\mathrm{i}^l}{kr}\sin(kr-\frac{1}{2}\pi l) + \mathcal{O}\left(\frac{1}{(kr)^2}\right) \end{align*}$$其中利用了 $P_l(1)1$ 和 $P_l(-1)(-1)^l =e^{\mathrm{i}\pi l}$.
所以展开系数为
那么就求得了平面波展开
$$\begin{align} e^{\mathrm{i}kr\cos\theta} \sim& \sum_{l=0}^{\infty} \frac{(2l+1)\mathrm{i}^l}{kr}\sin(kr-\frac{1}{2}\pi l) \cdot P_l(\cos\theta)\\ =& \sum_{l=0}^{\infty} \frac{(2l+1)}{2\mathrm{i}kr}\left( e^{\mathrm{i}kr}-e^{-\mathrm{i}kr} e^{\mathrm{i}\pi l} \right) P_l(\cos\theta)\quad \quad \mathrm{as}\quad r \to \infty\cdot \end{align}$$Wave Function as $r \to \infty$
设入射波函数为 $\Psi$ ,它可以是不同分波的本征波函数的任意叠加, 即
$$\begin{align} \Psi = \sum_{l = 0}^{+\infty} \frac{\chi_{kl}(r)}{kr}P_l(\cos\theta) \end{align}$$径向方程为
$$\begin{align} \frac{\mathrm{d}^2}{\mathrm{d}r^2}\chi -\left[ \frac{2\mu}{\hbar^2} V(r) - k^2 +\frac{l(l + 1)}{r^2}\right]\chi =0 \end{align}$$它在 $r\to\infty$ 时的解为
$$\begin{align} \Psi \sim& \sum_{l = 0}^{ + \infty} A_{l}\frac{1}{kr}\sin(kr-l\pi/2 + \delta_l)P_l(\cos\theta) \\ =& \sum_{l = 0}^{ + \infty} A_{l}\frac{1}{2\mathrm{i}kr} \left[ e^{\mathrm{i}(kr-\pi l/2 +\delta_{l})} -e^{-\mathrm{i}(kr-\pi l/2 +\delta_{l})} \right]P_l(\cos\theta) \end{align}$$同时, 当 $r\to\infty$ 时, 波函数可以写成入射平面波和散射波叠加的形式
$$\begin{align} \Psi \sim e^{\mathrm{i}kz} +f(\theta)\frac{e^{\mathrm{i}kr}}{r} \quad \quad \mathrm{as}\quad r\to \infty \end{align}$$将前面平面波的展开式代入上式得
$$\begin{align} \Psi \sim \sum_{l=0}^{\infty} \frac{(2l+1)}{2\mathrm{i}kr}\left( e^{\mathrm{i}kr}-e^{-\mathrm{i}kr} e^{\mathrm{i}\pi l} \right) P_l(\cos\theta) +f(\theta)\frac{e^{\mathrm{i}kr}}{r} \end{align}$$Partial-Wave Expansion
比较下列两式
$$\begin{align} \Psi \sim& \sum_{l = 0}^{ + \infty} A_{l}\frac{1}{2\mathrm{i}kr} \left[ e^{\mathrm{i}(kr-\pi l/2 +\delta_{l})} -e^{-\mathrm{i}(kr-\pi l/2 +\delta_{l})} \right]P_l(\cos\theta)\\ \Psi \sim& \sum_{l=0}^{\infty}\left[ \frac{(2l+1)}{2\mathrm{i}kr}\left( e^{\mathrm{i}kr}-e^{-\mathrm{i}kr} e^{\mathrm{i}\pi l} \right) P_l(\cos\theta)\right] +f(\theta)\frac{e^{\mathrm{i}kr}}{r} \end{align}$$对比 $e^{-\mathrm{i}kr}$ 的系数
$$\begin{align} \sum_{l = 0}^{ + \infty} A_{l}\frac{1}{2\mathrm{i}kr} e^{-\mathrm{i}(kr-\pi l/2 +\delta_{l})}P_l(\cos\theta) =\sum_{l=0}^{\infty} \frac{(2l+1)}{2\mathrm{i}kr}e^{-\mathrm{i}kr} e^{\mathrm{i}\pi l} P_l(\cos\theta) \end{align}$$可得
$$\begin{align} A_l = \mathrm{i}^l (2l+1)e^{\mathrm{i}\delta_l} \end{align}$$对比 $e^{\mathrm{i}kr}$ 的系数
$$\begin{align} \sum_{l = 0}^{ + \infty} A_{l}\frac{1}{2\mathrm{i}kr} e^{\mathrm{i}(kr-\pi l/2 +\delta_{l})} P_l(\cos\theta) = \sum_{l=0}^{\infty}\left[ \frac{(2l+1)}{2\mathrm{i}kr} e^{\mathrm{i}kr} P_l(\cos\theta)\right] +f(\theta)\frac{e^{\mathrm{i}kr}}{r} \end{align}$$可得
$$\begin{align} f(\theta) = \sum_{l = 0}^{ + \infty} \frac{2l+1}{2\mathrm{i}k} \left(e^{\mathrm{i}\cdot2\delta_{l}} -1\right) P_l(\cos\theta) \end{align}$$$l=0$
当 $l=0$ 时
$$\begin{align} f_s(\theta) = \frac{e^{2\mathrm{i}\delta_l}-1}{2\mathrm{i}k} = -\frac{1}{\mathrm{i}k-k/\tan\delta} = -\frac{1}{1/a_s +\mathrm{i}k} \end{align}$$Supplementary
Reference
Arfken, Weber, Harris, Mathematical Methods for Physicists 7ed:
- Chap 7.5 Series Solutions-Frobenius' Methods
- Example 8.3.1 Legendre Equation
- Chap 9.4 Separation of Variables, Spherical Polar Coordinates
- Chap 15.2 Orthogonality (Legendre Functions)
C. J. Pethick, H. Smith, Bose-Einstein Condensation in Dilute Gases
- Chap 5.2 Basic Scattering Theory
