---
问题积分
\[ \begin{align} I(\Omega) =& \frac{1}{2\pi}\int_0^{\infty}\mathrm{d}^3\vec{q}\cdot \mathrm{Im} \left[\frac{1}{q^2-16q\cos\theta+2(\Omega+14)+\mathrm{i}0^+}\right]\\ =& \frac{1}{2\pi}\int_0^{\infty}\mathrm{d}q \int_0^{\pi}\mathrm{d}\theta \int_0^{2\pi}\mathrm{d}\phi \cdot \mathrm{Im} \left[\frac{q^2\sin\theta} {q^2-16q\cos\theta+2(\Omega+14)+\mathrm{i}0^+}\right]\\ =&\int_0^{\infty}\mathrm{d}q\int_{-1}^1\mathrm{d}x \cdot\mathrm{Im}\left[ \frac{q^2}{q^2-16qx+2(\Omega+14)+\mathrm{i}0^+} \right] \end{align} \]全部解析地积: 先积 \(x\) 再积 \(q\)
\[ \begin{align} I(\Omega) =&\int_0^{\infty}\mathrm{d}q \cdot \frac{q}{16}\mathrm{Im}\left[ \ln\left(q^2+16q+2(\Omega+14)+\mathrm{i}0^+\right) -\ln\left(q^2-16q+2(\Omega+14)+\mathrm{i}0^+\right) \right] \\ =& -\pi \theta(18-\Omega)\sqrt{2(18-\Omega)} \end{align} \]全部解析地积: 先积 \(q\) 对积 \(x\)
\[ \begin{align} I(\Omega) =&-\pi\int_{-1}^1\mathrm{d}x \int_0^{\infty}\mathrm{d}q\cdot q^2\frac{\delta(q-q^+)+\delta(q-q^-)}{|q^+-q^-|}\\ =&-\pi\left[\int_{-1}^1\mathrm{d}x \cdot\frac{\theta(-\Omega-14)q^{+2}}{|q^+-q^-|} +\int_\sqrt{\frac{\Omega+14}{32}}^1\mathrm{d}x\cdot \frac{\theta(\Omega+14)\theta(18-\Omega) \left( q^{+2}+q^{-2} \right)}{|q^+-q^-|}\right]\\ =& -\pi\theta(18-\Omega)\sqrt{2(18-\Omega)} \end{align} \]解析积 \(q\) , 数值积 \(x\)
\[ \begin{align} I(\Omega) =&-\pi\int_{-1}^1\mathrm{d}x \int_0^{\infty}\mathrm{d}q\cdot q^2\frac{\delta(q-q^+)+\delta(q-q^-)}{|q^+-q^-|}\\ =&\int_0^{\infty}\mathrm{d}q\int_{-1}^1\mathrm{d}x \cdot\mathrm{Im}\left[ \frac{q^2}{q^2-16qx+2(\Omega+14)+\mathrm{i}0^+} \right](通否化成 q 复平面上的积分?)\\ =&-\pi\left[\int_{-1}^1\mathrm{d}x \cdot\frac{\theta(-\Omega-14)q^{+2}}{|q^+-q^-|} +\int_\sqrt{\frac{\Omega+14}{32}}^1\mathrm{d}x\cdot \frac{\theta(\Omega+14)\theta(18-\Omega) \left( q^{+2}+q^{-2} \right)}{|q^+-q^-|}\right] \end{align} \]其中
\[ \begin{align} \Delta =& (16x)^2-8(\Omega+14) \\ q^{\pm} =& \frac{16x \pm\sqrt{\Delta}}{2} \end{align} \]而
\[ |q^+ - q^-| = \sqrt{\Delta} \] \[ \begin{align} \int_{-1}^{1}\mathrm{d}x\cdot\frac{q^{+2}}{|q^+-q^-|} =& \frac{1}{4}\int_{-1}^{1}\mathrm{d}x\cdot\left(32x + \sqrt{\Delta}+\frac{(16x)^2}{\sqrt{\Delta}}\right) \\ =& \frac{1}{4}\int_{-1}^{1}\mathrm{d}x\cdot\left(32x + \sqrt{(16x)^2-8(\Omega+14)}+ \frac{(16x)^2}{\sqrt{(16x)^2-8(\Omega+14)}}\right) \end{align} \] \[ \begin{align} \int_\sqrt{\frac{\Omega+14}{32}}^1\mathrm{d}x\cdot\frac{q^{+2}+q^{-2}}{|q^+-q^-|} =& \frac{1}{2}\int_\sqrt{\frac{\Omega+14}{32}}^1\mathrm{d}x\cdot\frac{(16x)^2+ \Delta}{\sqrt{\Delta}} \\ =& \frac{1}{2}\int_\sqrt{\frac{\Omega+14}{32}}^1\mathrm{d}x\cdot\left[\frac{(16x)^2}{\sqrt{\Delta}} +\sqrt{\Delta}\right] \\ =& \frac{1}{2}\int_\sqrt{\frac{\Omega+14}{32}}^1\mathrm{d}x\cdot\left[\frac{(16x)^2}{\sqrt{(16x)^2-8(\Omega+14)}} +\sqrt{(16x)^2-8(\Omega+14)}\right] \end{align} \]上面这两个积分, 想通过数值计算. 值得注意的是, 被积函数在积分下限处发散, 但是 \(\mathcal{O}\left(x^{-\frac{1}{2}}\right)\) 形式的发散, 积分结果并不发散. 比如当 \(\Omega=-6\) 时
\[ \begin{align} \int_\sqrt{\frac{\Omega+14}{32}}^1\mathrm{d}x\cdot\frac{q^{+2}+q^{-2}}{|q^+-q^-|} =& \frac{1}{2}\int_\sqrt{\frac{\Omega+14}{32}}^1\mathrm{d}x\cdot\left[\frac{(16x)^2}{\sqrt{(16x)^2-8(\Omega+14)}} +\sqrt{(16x)^2-8(\Omega+14)}\right] \\ =& \frac{1}{2}\int_\frac{1}{2}^1\mathrm{d}x\cdot\left[\frac{(16x)^2}{\sqrt{(16x)^2-64}} +\sqrt{(16x)^2-64}\right] \end{align} \]普遍情况
积分
\[ I(B,C,x) = \int_{0}^{\infty}\mathrm{d}q\cdot \mathrm{Im}\left[ \frac{q^2f(q)}{q^2 - qBx+C+\mathrm{i}0^+}\right] ,\quad \mathrm{for} \,\, x\in[-1,1],B>0 \]分母中关于 \(q\) 的二次函数的根的判别式
\[ \begin{align} \Delta =& (Bx)^2 -4C \\ \Delta >& 0 \Rightarrow C<\frac{(Bx)^2}{4} \\ \end{align} \]只有 \(\Delta>0\) 时, 积分才不为零. 此时分母中关于 \(q\) 的二次函数有两个根
\[ q^{\pm} = \frac{Bx\pm\sqrt{\Delta}}{2} \]取虚部
\[ \begin{align} I(B,C,x) =& -\pi\int_0^{\infty}\mathrm{d}q\cdot q^2f(q)\frac{\delta(q-q^+)+\delta(q-q^+)}{|q^+-q^-|} \\ =& -\pi\int_0^{\infty}\mathrm{d}q\cdot q^2f(q)\frac{\delta(q-q^+)+\delta(q-q^+)}{\sqrt{\Delta}} \end{align} \]对 \(q\) 的积分范围是 \([0, \infty]\) , 因此 \(q^{\pm}>0\) 时, 对应的 Dirac delta 函数才对积分有贡献.
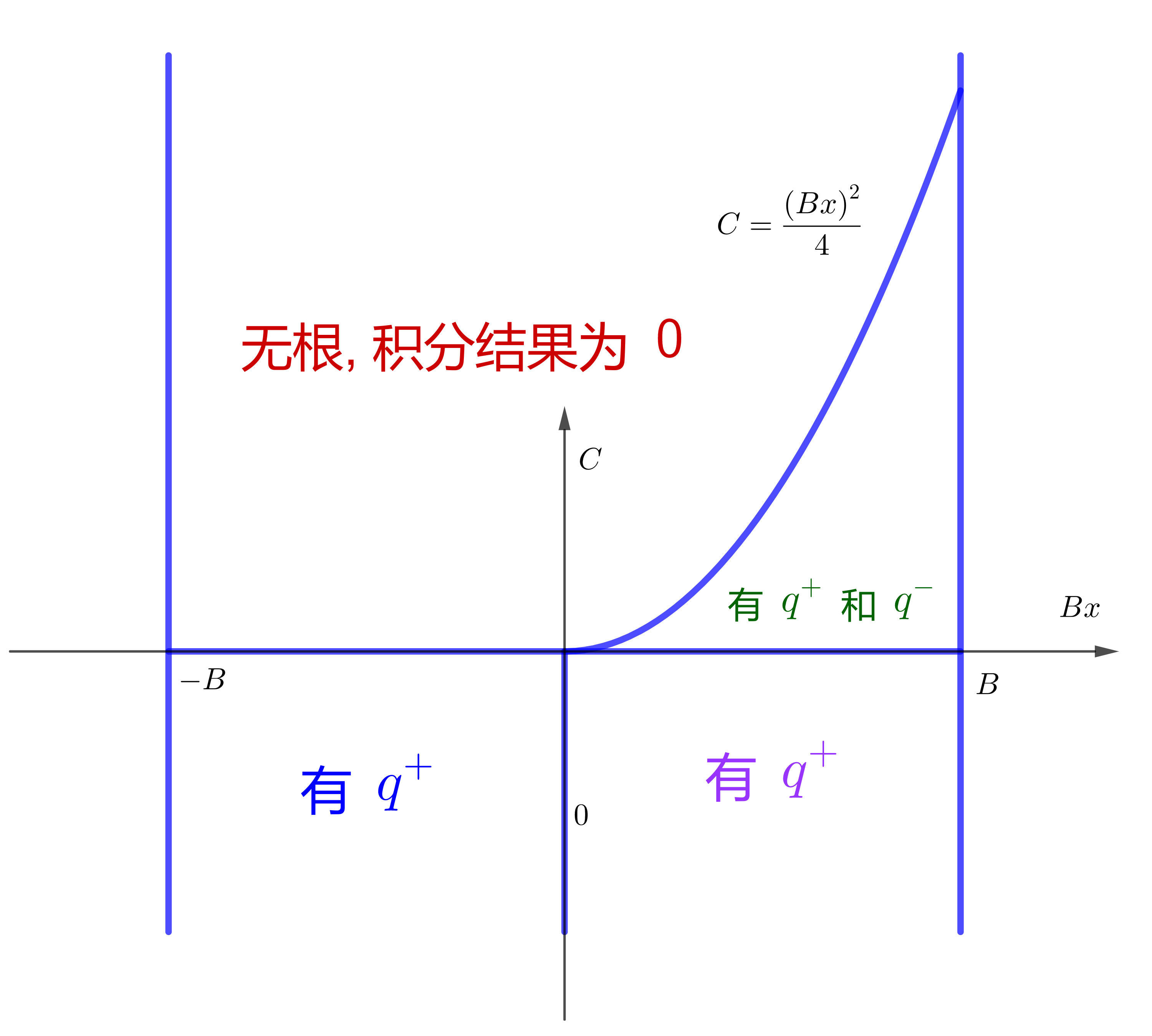
\(q^+>0\) 的条件为
-
当 \(x>0\) 时: \(q^+>0\) 恒成立.
-
当 \(x < 0\) 时: 若要 \(q^+ > 0\) , 应有 \(Bx+\sqrt{\Delta}>0 \Rightarrow C<0\) .
\(q^->0\) 的条件为
- 当 \(x < 0\) 时: \(q ^ - < 0\) 恒成立, 即 \(q^+ > 0\) 恒不成立.
- 当 \(x>0\) 时: 若要 \(q^->0\) 应有 \(Bx-\sqrt{\Delta}>0 \Rightarrow C>0\) .
所以对积分有贡献的区域如下图
因此, 积分化为
\[ \begin{align} I(B,C,x) =& -\pi\int_0^{\infty}\mathrm{d}q\cdot q^2f(q)\frac{\delta(q-q^+)+\delta(q-q^+)}{\sqrt{\Delta}} \\ =& -\pi \left[ \theta(-C)\frac{f(q^+)q^{+2}}{\sqrt{\Delta}} + \theta(C)\theta\left(\frac{(Bx)^2}{4}-C\right) \theta\left(\sqrt{\frac{4C}{B}}-x\right) \frac{f(q^+)q^{+2}+f(q^-)q^{-2}}{\sqrt{\Delta}}\right] \end{align} \]Supplementary
先积 \(x\) 再积 \(q\) 的详细过程
\[ \begin{align}I(\Omega) =&\int_0^{\infty}\mathrm{d}q \cdot \frac{q}{16}\mathrm{Im}\left[ \ln\left(q^2+16q+2(\Omega+14)+\mathrm{i}0^+\right) -\ln\left(q^2-16q+2(\Omega+14)+\mathrm{i}0^+\right) \right] \\ =& -\pi \theta(18-\Omega)\sqrt{2(18-\Omega)}\end{align} \]上式中第二个等号的计算细节.
只有当第一个对数中大于零, 第二个对数中小于零时积分才不为零.
二次函数根的判别式相同, 为
\[ \begin{align} \Delta = 16^2-8(\Omega + 14)\\ \Delta > 0 \Rightarrow \Omega < 18 \\ \sqrt{\Delta} > 16 \Rightarrow \Omega < 14 \end{align} \]第一项的根为
\[ q^{\pm}= \frac{-16 \pm \sqrt{\Delta}}{2} \]第二项的根为
\[ q^{\pm}= \frac{16 \pm \sqrt{\Delta}}{2} \]积分不为零的条件为
\[ \begin{align} 0<\frac{\sqrt{\Delta}-16}{2}<q<\frac{\sqrt{\Delta}+16}{2},\quad \mathrm{if}\quad \sqrt{\Delta}>14 \\ 0<\frac{16-\sqrt{\Delta}}{2}<q<\frac{16+\sqrt{\Delta}}{2},\quad \mathrm{if}\quad \sqrt{\Delta}<14 \end{align} \]所以积分结果为
\[ \begin{align} I(\Omega) =& -\pi\left[ \theta(14-\Omega)\left.\frac{q^2}{32}\right|_{q=\frac{\sqrt{\Delta}-16}{2}}^{q=\frac{\sqrt{\Delta}+16}{2}} +\theta(\Omega-14)\theta(18-\Omega)\left.\frac{q^2}{32}\right|_{q=\frac{16-\sqrt{\Delta}}{2}}^{q =\frac{16+\sqrt{\Delta}}{2}} \right]\\ =&-\pi \theta(18-\Omega)\frac{\sqrt{\Delta}}{2} \\ =& -\pi \theta(18-\Omega)\sqrt{2(18-\Omega)} \end{align} \]先积 \(q\) 再积 \(x\) 的详细过程
\[ \begin{align} I(\Omega) =&-\pi\int_{-1}^1\mathrm{d}x \int_0^{\infty}\mathrm{d}q\cdot q^2\frac{\delta(q-q^+)+\delta(q-q^-)}{|q^+-q^-|}\\ =&-\pi\left[\int_{-1}^1\mathrm{d}x \cdot\frac{\theta(-\Omega-14)q^{+2}}{|q^+-q^-|} +\int_\sqrt{\frac{\Omega+14}{32}}^1\mathrm{d}x\cdot \frac{\theta(\Omega+14)\theta(18-\Omega) \left( q^{+2}+q^{-2} \right)}{|q^+-q^-|}\right]\\ =& -\pi \left[ \theta(-\Omega-14)\left.\cdot \frac{x}{4} \sqrt{(16x)^2-8(\Omega+14)}\right|_{x=-1}^{x=1} \\ +\left.\theta(\Omega+14)\theta(18-\Omega)\cdot \frac{x}{2} \sqrt{(16x)^2-8(\Omega+14)}\right|_{x=\sqrt{\frac{\Omega+14}{32}}}^{x=1} \right]\\ =& -\pi \left[ \theta(-\Omega-14)\left.\cdot \frac{x}{2} \sqrt{(16x)^2-8(\Omega+14)}\right|_{x=0}^{x=1} \\ +\left.\theta(\Omega+14)\theta(18-\Omega)\cdot \frac{x}{2} \sqrt{(16x)^2-8(\Omega+14)}\right|_{x=\sqrt{\frac{\Omega+14}{32}}}^{x=1} \right]\\ =& -\pi \left[ \theta(-\Omega-14)\left.\cdot \frac{x}{2} \sqrt{(16x)^2-8(\Omega+14)}\right|_{x=0}^{x=1} \\ +\left.\theta(\Omega+14)\theta(18-\Omega)\cdot \frac{x}{2} \sqrt{(16x)^2-8(\Omega+14)}\right|_{x=\sqrt{\frac{\Omega+14}{32}}}^{x=1} \right] \\ =& -\pi\theta(18-\Omega)\sqrt{2(18-\Omega)} \end{align} \]总结
数值积分的时候, 注意某个点发散但积分不发散的情况.
