p-Wave Scattering Amplitude
由 Taylor 书 (6.14) 可得 $l$ 分波的散射振幅
$$\begin{align} f_l(k) = \frac{e^{2\mathrm{i}\delta_l(k)} - 1}{2 \mathrm{i} k} = \frac{1}{k \cot \delta_l(k) - \mathrm{i}k} \end{align}$$对于 $l = 1$ 的 p 波, 用 $m = 1, 0, -1$ 表示磁量子数, 将 $k^3\cot \delta_m(k)$ 低能展 开到 $k^2$ 阶
$$\begin{align} k^3\cot \delta_m(k) = - \frac{1}{v_m} - \frac{k^2}{R_m} \end{align}$$其中 $v_m$ 是 effective volume, $R_m$ 是 effective range. 那么散射振幅就为
$$\begin{align} \label{eq:scatterAM} f(k) \approx \frac{k^2}{- \frac{1}{v_m} - \frac{k^2}{R_m} - \mathrm{i}k^3} \end{align}$$Hamiltonian
考虑 p 波相互作用的两分量 Bose 气体
$$\begin{align} \hat{H} = &\sum_{\vec{k},\sigma}\left(\frac{k^2}{2M} - \mu\right)\hat{a}_{\vec{k},\sigma}^{\dagger} \hat{a}_{\vec{k},\sigma} + \sum_{\vec{q},m}\left(\frac{q^2}{4M} - 2 \mu - \nu_m\right)\hat{b}_{\vec{q},m}^{\dagger} \hat{b}_{\vec{q}, m}\\ &+ \sqrt{\frac{1}{V }} \sum_{\vec{k},\vec{q},m}\left[g_m k Y_{1, m}(\hat{k}) \hat{b}^{\dagger}_{\vec{q},m}\hat{a}_{\frac{\vec{q}}{2} + \vec{k}} \hat{a}_{\frac{\vec{q}}{2} - \vec{k}} + \mathrm{h.c.} \right] \end{align}$$T-matrix
下图中 $G_0$ 表示自由原子的自由松原格林函数, $D_0$ 表示两个原子形成的分子的自由 松原格林函数, $D$ 表示考虑分子分裂和形成之后的分子格林函数
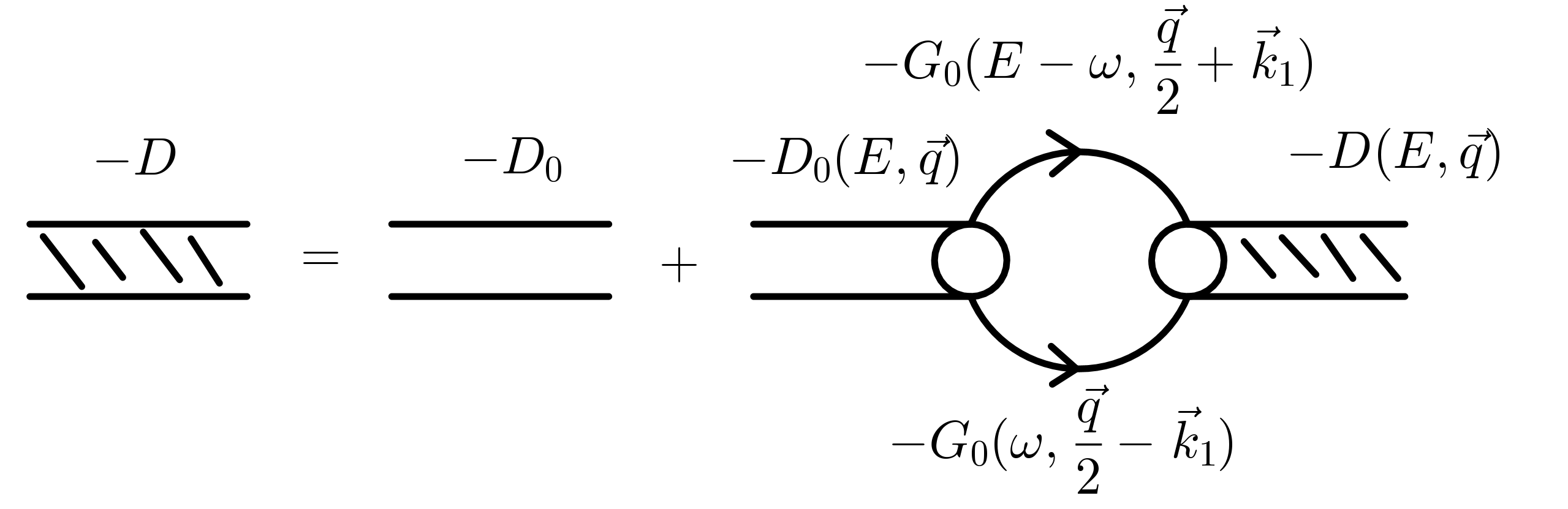
通过图可以对应 Dyson 方程
$$\begin{align} D = D_0-D_0 \left(\frac{1}{\beta}\sum_{\vec{k}_1, \omega}\mathcal{V} G_1 G_2\mathcal{V}^* \right) D \end{align}$$其中 $\mathcal{V}$ 表示 p 波相互作用顶点. 即 $\mathcal{V} = \frac{1}{\sqrt{V}}g_m k Y_{1, m}(\hat{k})$ . 通过此 Dyson 方程可以得到分子格林函 数的表达式为
$$\begin{align} \frac{1}{D} = \frac{1}{D_0} + \frac{1}{\beta}\sum_{\vec{k}_{1}, \omega} G_0 G_0|\mathcal{V}|^2 \end{align}$$其中对 $\omega$ 的求和可以由 Matsubara frequency summation 求出(考虑化学势会影响重整 化关系?)
$$\begin{align} &\frac{1}{\beta}\sum_{\vec{k}_{1}, \omega} G_{0}(E - \omega, \frac{\vec{q}}{2} + \vec{k}_1) G_0(\omega, \frac{\vec{q}}{2} - \vec{k}_1)|\mathcal{V}|^2\\ =& -\sum_{\vec{k}_1} \frac{n(\varepsilon_{\vec{q} /2 + \vec{k}_1})+1 + n(\varepsilon_{\vec{q}/2 - \vec{k}_1})} {\mathrm{i}E- \varepsilon_{\vec{q} /2 + \vec{k}_1} - \varepsilon_{\vec{q} /2 - \vec{k}_1}} \frac{1}{V } g_m^2 k_1^2 \left|Y_{l, m}(\hat{k}_1)\right|^2\\ \end{align}$$所以求得分子松原格林函数
$$\begin{align} \frac{1}{D} = \mathrm{i}E - \frac{q^2}{4M} + \nu_m -\sum_{\vec{k}_1} \frac{n(\varepsilon_{\vec{q} /2 + \vec{k}_1})+1 + n(\varepsilon_{\vec{q}/2 - \vec{k}_1})} {\mathrm{i}E- \varepsilon_{\vec{q} /2 + \vec{k}_1} - \varepsilon_{\vec{q} /2 - \vec{k}_1}} \frac{1}{V } g_m^2 k_1^2 \left|Y_{l=1, m}(\hat{k}_1)\right|^2 \end{align}$$将松原格林函数解析延拓成推迟格林函数(忽粒子数是延拓的一部分?)
$$\begin{align} \frac{1}{D^{\mathrm{ret}}} = E + \mathrm{i}0^+ - \frac{q^2}{4M} + \nu_m -\sum_{\vec{k}_1} \frac{1} {E + \mathrm{i}0^+ - \varepsilon_{\vec{q} /2 + \vec{k}_1} - \varepsilon_{\vec{q} /2 - \vec{k}_1}} \frac{1}{V } g_m^2 k_1^2 \left|Y_{1, m}(\hat{k}_1)\right|^2 \end{align}$$因此可以得到 T-matrix 为(不仅加上两个顶点, 还要有个因子 $4$ ?)(以及求和项中 $4\pi$ 的来源?)
$$\begin{align} T(k \hat{k}, k \hat{k}', E = \frac{k^2}{M}) =& \frac{1}{V} g_m^{2}k^2 Y_{1, m}^{*}(\hat{k}) Y_{1, m}(\hat{k}') D^{\mathrm{ret}}(\vec{q} = 0, E) \\ =& \frac{\frac{1}{V} g_m^{2}k^2 Y_{1, m}^{*}(\hat{k}) Y_{1, m}(\hat{k}')} {E + \mathrm{i}0^+ + \nu_m - 4\pi \sum_{\vec{k}_1} \frac{g_m^2 k_1^2\left|Y_{1, m}(\hat{k_1})\right|^2}{V} \frac{1}{E - \frac{k_1^2}{M} + \mathrm{i}0^+}} \end{align}$$Renormalization
分母中的求和化积分为(球谐函数对角度积分归一)
$$\begin{align} &4\pi \sum_{\vec{k}_1} \frac{g_m^2 k_1^2\left|Y_{1, m}(\hat{k_1})\right|^2}{V} \frac{1}{E - \frac{k_1^2}{M} + \mathrm{i}0^+} \\ =& \frac{g_m^2}{2 \pi^2}\int_0^{\infty} \mathrm{d}k_1 \frac{k^4_1}{E- \frac{k_1^2}{M} + \mathrm{i}0^+} \\ =& \frac{g_m^2}{2 \pi^2}\int_0^{\infty} \mathrm{d}k_1 \left[\mathcal{P}\frac{k^4_1}{E- \frac{k_1^2}{M}} - \mathrm{i}\pi \cdot k_1^4 \delta(E - \frac{k_1^2}{M})\right] \end{align}$$被积函数部分发散, 其发散行为
$$\begin{align} \frac{k^4_1}{E- \frac{k_1^2}{M}} = - M^2E - Mk_1^2 + M^2 E^2 \frac{1}{E - \frac{k_1^2}{M}} \end{align}$$第一项是常数, 第二项是 $k^2$ , 对这两项的积分是发散的. 而第三项, 可以算出其积分值 为 $0$ . 被积函数虚部可以算出
$$\begin{align} - \mathrm{i}\pi \int_0^{\infty} \mathrm{d}k_1 \cdot k_1^4 \delta(E - \frac{k_1^2}{M}) = -\mathrm{i}\pi \frac{M k^3}{2} \end{align}$$其中利用了关系 $E = \frac{k^2}{M}$ .
将积分结果代回原式, 并将积分再化为求和, 得
$$\begin{align} &4\pi \sum_{\vec{k}_1} \frac{g_m^2 k_1^2\left|Y_{1, m}(\hat{k_1})\right|^2}{V} \frac{1}{E - \frac{k_1^2}{M} + \mathrm{i}0^+} \\ =& - \frac{g_m^2}{V} M \left[\sum_{\vec{k}_1} \frac{ME}{k^2_1} + \sum_{\vec{k}_1}1 \right] - \mathrm{i} \frac{g_m^2}{4\pi} Mk^3 \end{align}$$将此结果代加 T-matrix 表达式可得
$$\begin{align} T(k \hat{k}, k \hat{k}', E = \frac{k^2}{M}) =& \frac{\frac{1}{V} k^2 Y_{1, m}^{*}(\hat{k}) Y_{1, m}(\hat{k}')} {\frac{k^2}{M }\left[ \frac{1}{g_m^2} + \frac{M^2}{V}\sum_{\vec{k}_1}\frac{1}{k_1^2}\right] + \left[ \frac{\nu_m}{g_m^2} + \frac{M}{V}\sum_{\vec{k}_1}1 \right] + \mathrm{i} \frac{M}{4\pi}k^3 } \end{align}$$其中利用了关系 $E = \frac{k^2}{M}$ . 上式与 (\ref{eq:scatterAM}) 对比可得重整化关 系
$$\begin{align} \frac{1}{g_m^2} =& \frac{M^2}{4\pi} R_m^{-1} - \frac{M^2}{V}\sum_{\vec{k}_1}\frac{1}{k_1^2} \\ \frac{\nu_m}{g_m^2} = & \frac{M}{4\pi} v_m^{-1} - \frac{M}{V} \sum_{\vec{k}_1}1 \end{align}$$重整化之后的 T-matrix 为 \begin{align} T(k \hat{k}, k \hat{k}', E = \frac{k^2}{M}) =& \frac{\frac{1}{V} R_m \frac{4\pi}{M^2}k^2 Y_{1, m}^{*}(\hat{k}) Y_{1, m}(\hat{k}')} {\frac{k^2}{M } + \frac{R_m}{M v_m} + \mathrm{i} \frac{R_m}{M }k^3 } \end{align}
Reference
- Taylor, Scattering Theory: quantum theory of nonrelativistic collisions, 1972, John Wiley & Sons
- PhysRevA.86.012711, Renormalization in the three-body problem with resonant p-wave interactions
- PhysRevA.99.012701, Three-body problem of bosons near a d-wave resonance
