Hamiltonian

Nuclear Spin $I$ , orbital angular momentum $L$ , and $spin$ is

$$\begin{align*} I =& \frac{3}{2} \\ L =& 0 \\ S =& \frac{1}{2} \\ \end{align*}$$

Hamiltonian is

$$\begin{align*} H_S =& A \vec{I} \cdot \vec{J} + C J_z +D I_z \\ =& A \left[ I_z J_z + \frac{1}{2}(I_{ +}J_- +I_-J_{ +}) \right] + C J_z + D I_z \end{align*}$$ $$\begin{align*} |1\rangle =& |\frac{3}{2},\frac{1}{2}\rangle \\ |2\rangle =& |\frac{1}{2},\frac{1}{2}\rangle \\ |3\rangle =& |-\frac{1}{2},\frac{1}{2}\rangle \\ |4\rangle =& |-\frac{3}{2},\frac{1}{2}\rangle \\ |5\rangle =& |\frac{3}{2},-\frac{1}{2}\rangle \\ |6\rangle =& |\frac{1}{2},-\frac{1}{2}\rangle \\ |7\rangle =& |-\frac{1}{2},-\frac{1}{2}\rangle \\ |8\rangle =& |-\frac{3}{2},-\frac{1}{2}\rangle \\ \end{align*}$$

Hamiltonian in the Hilbert space spaned by above kets is

$\mid 1 \rangle$ $\mid 2 \rangle$ $\mid 3 \rangle$ $\mid 4 \rangle$ $\mid 5 \rangle$ $\mid 6 \rangle$ $\mid 7 \rangle$ $\mid 8 \rangle$
$\langle 1 \mid$ $\frac{3}{4}A+\frac{1}{2}C+\frac{3}{2}D$ $0$ $0$ $0$ $0$ $0$ $0$ $0$
$\langle 2 \mid$ $0$ $\frac{1}{4}A+\frac{1}{2}C+\frac{1}{2}D$ $0$ $0$ $\frac{\sqrt{3}}{2}A$ $0$ $0$ $0$
$\langle 3 \mid$ $0$ $0$ $-\frac{1}{4}A+\frac{1}{2}C-\frac{1}{2}D$ $0$ $0$ $A$ $0$ $0$
$\langle 4 \mid$ $0$ $0$ $0$ $-\frac{3}{4}A+\frac{1}{2}C-\frac{3}{2}D$ $0$ $0$ $\frac{\sqrt{3}}{2}A$ $0$
$\langle 5 \mid$ $0$ $\frac{\sqrt{3}}{2}A$ $0$ $0$ $-\frac{3}{4}A-\frac{1}{2}C+\frac{3}{2}D$ $0$ $0$ $0$
$\langle 6 \mid$ $0$ $0$ $A$ $0$ $0$ $-\frac{1}{4}A-\frac{1}{2}C+\frac{1}{2}D$ $0$ $0$
$\langle 7 \mid$ $0$ $0$ $0$ $\frac{\sqrt{3}}{2}A$ $0$ $0$ $\frac{1}{4}A-\frac{1}{2}C-\frac{1}{2}D$ $0$
$\langle 8 \mid$ $0$ $0$ $0$ $0$ $0$ $0$ $0$ $\frac{3}{4}A-\frac{1}{2}C-\frac{3}{2}D$

Numerical Results

Python code

import numpy as np
import sympy as sym
from matplotlib import pyplot as plt

# Hamiltonian is H = a*I*J + c*J_z + d*I_z
a = 4000000

def H(B):
    c = 4000*B
    d = 4*B

    H = np.zeros([8,8])      #Hamiltonian in direct production Hilbert space

    H[0,0] =  3/4*a +  1/2*c +  3/2*d
    H[7,7] =  3/4*a -  1/2*c -  3/2*d

    H[1,1] =  1/4*a +  1/2*c +  1/2*d
    H[2,2] = -3/4*a -  1/2*c +  3/2*d
    H[1,2] =  np.sqrt(3)/2*a
    H[2,1] = H[1,2]

    H[3,3] = -1/4*a +  1/2*c -  1/2*d
    H[4,4] = -1/4*a -  1/2*c +  1/2*d
    H[3,4] =  a
    H[4,3] = H[3,4]

    H[5,5] = -3/4*a +  1/2*c -  3/2*d
    H[6,6] =  1/4*a -  1/2*c -  1/2*d
    H[5,6] =  np.sqrt(3)/2*a
    H[6,5] = H[5,6]
#    np.set_printoptions(precision=1)
    [x,y] = np.linalg.eig(H)  #Diagnolization the Hamiltonian
    x = np.sort(x)
    return x

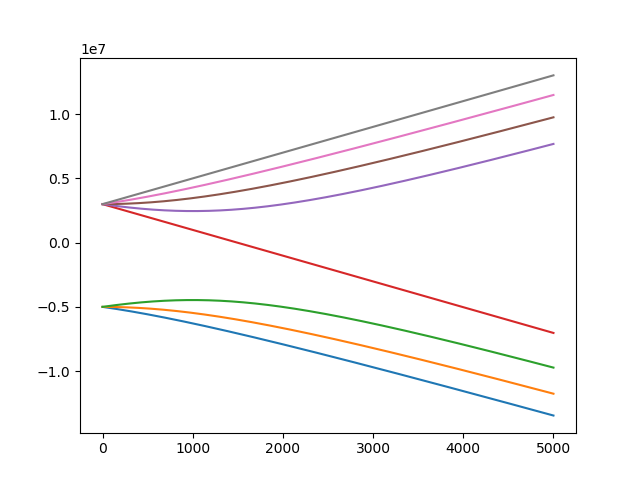
N = 2000
bmax = 5000        #the upper limit of magnetic field
b = np.linspace(0,bmax,N)
E = np.zeros([8,N])  #the eight eigenvaluses of energy , as a function of magnetic field
for i in range(8):
    for j in range(N):
        E[i,j] = H(b[j])[i]
    plt.plot(b,E[i])

plt.show()

#+RESULTS: : None

Results

rb87_HFS

Reference

C. J. Pethick, H. Smith, Bose-Einstein Codensation in Dilute Gases