挖个坑，之后慢慢填。
一维方势阱

import numpy as np
import matplotlib.pyplot as plt

def S(E, V0, a):
    """0<E<V0
    曾谨言. 量子力学（卷1）, 2007. Eq(3.3.15)
    """
    k = np.sqrt(2*E)
    K = np.sqrt(2*(V0-E))
    S_val = -2j*k/K
    S_val /= (1 - (k/K)**2) * np.sinh(K*a) - 2j*k/K*np.cosh(K*a)
    S_val *= np.exp(-1j*k*a)
    return S_val

def R(E, V0, a):
    """0<E<V0"""
    k = np.sqrt(2*E)
    K = np.sqrt(2*(V0-E))
    R_val = S(E, V0, a) * (1+1j*k/K) * np.exp(1j*k*a - K*a)
    R_val -= 1+1j*k/K
    R_val /= 1-1j*k/K
    return R_val

def f_kk(E, V0, a):
    return (S(E, V0, a)-1)*2*np.pi/1j

def f_mkk(E, V0, a):
    return R(E, V0, a)*2*np.pi*1j

def sigma_total(E, V0, a):
    k = np.sqrt(2*E)
    return (np.abs(f_kk(E, V0, a))**2 + np.abs(f_mkk(E, V0, a))**2)/k

def sigma_total_optical_theorems(E, V0, a):
    k = np.sqrt(2*E)
    return 4*np.pi*f_kk(E, V0, a).imag/k

a = 0.2
V0 = 5
Es = np.linspace(1e-2, V0, 100, endpoint=False)
Ss = []
Rs = []
sigma_total_s = []
optical_theorem_s = []
sigma_kk_s = []
sigma_mkk_s = []
f_kk_s = []
f_mkk_s = []
for ei in Es:
    Ss.append(S(ei, V0, a))
    Rs.append(R(ei, V0, a))
    sigma_total_s.append(sigma_total(ei, V0, a))
    optical_theorem_s.append(sigma_total_optical_theorems(ei, V0, a))
    sigma_kk_s.append(np.abs(f_kk(ei, V0, a))**2/np.sqrt(2*ei))
    sigma_mkk_s.append(np.abs(f_mkk(ei, V0, a))**2/np.sqrt(2*ei))
    f_kk_s.append(f_kk(ei, V0, a))
    f_mkk_s.append(f_mkk(ei, V0, a))

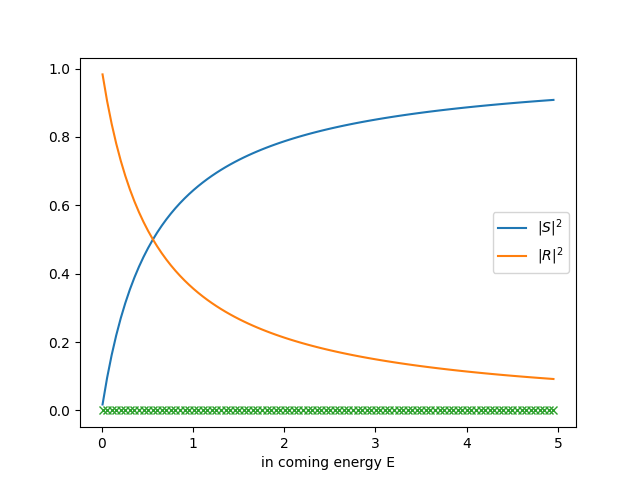
plt.plot(Es, np.abs(Ss)**2, label=r'$|S|^2$')
plt.plot(Es, np.abs(Rs)**2, label=r'$|R|^2$')
plt.plot(Es, ((np.array(Rs).conjugate())*np.array(Ss) - np.array(Rs)*(np.array(Ss).conjugate())).real, 'x')
plt.xlabel('in coming energy E')
plt.legend()
plt.savefig('fig.png', transparent=True)
image-scattering
参考资料

曾谨言. 量子力学（卷1）, 2007.
Scattering Summarize

一维方势阱

参考资料
